こんにちは。Horyです。
コンデンサの内容も終わって、いよいよ、電流や抵抗・電圧の関係などについて話すことになりました。やっと電気回路のことについて話せます。
ただ、その前に、これらを理解する技術的な事項として連続体近似という技術があります。
今回は電流の正体について解説すると共に、連続体近似という技術について原理と本質を紹介しようと思います。
今回も頑張りましょう。
電子が持つ電気量
私たちは、今までにコンデンサやガウスの法則で電場を求めてきました。
電場を求める時、電荷が受ける力を1つ1つ記述していたら収拾がつきません。何故なら、電荷の数自体が莫大だからです。
ところで、電子が持つ電気量は電荷の中で最小の単位でアルコとが知られています。これは数値も求まっていて以下のように表せます。
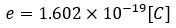
このeを我々は電気素量といって、導体の電気量とかはこれの整数倍で求めれます。
つまり、導体中の電子数が分かれば、導体が持つ電気量をQ=neのように求めれます。
電気素量は数値自体を暗記しても良いです。
連続体近似とその必要性
まずは、離散関数と連続関数の違いです。
- 離散関数・・・連続でない途切れ途切れの関数
- 連続関数・・・連続で途切れない関数
連続体近似とはその名の通り、ここでは、本来は離散関数である電気量を連続関数に近似するという意味です。
理由は離散関数だと計算が複雑だからです(離散関数は微分ができないし、扱いが厄介)。
まぁ、数学の話で連続関数だから微分が必ずできるかというとそうではないですが、数学の記事絵はないので、今回は微分できるとします。
電流の正体
電流を「特定の面を通過した全ての電子の電気量を時間で微分した量」と定義します。
要するに、「電流の正体は電荷の流れ」といっています。このように定義すると、電流は以下のように立式することが可能です。
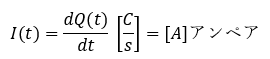
基本単位を電気量[C]ではなく、[A]としている専門書もあります。
位置エネルギー
電気量Q=neの電荷の位置エネルギーは導体における「電位差」をVとして以下のように示します。
電位差であることに注意してください。電位差なので位置の関数ではなく、電気量の関数です。
- 電位・・・電荷Qがあるとして、この電荷から無限に離れた点から1Cの電荷を運んだときのクーロン力による位置エネルギー (位置の関数)
- ・電位差・・・例えば、2点間を基準として、そのうちの一点を基準(0V)としたときに他方の電位はどのくらい?・・・ただの比較
電位差から位置エネルギーを求めると・・・
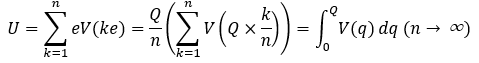
まぁ、ここまで言っても余りイメージが着かないと思うので分かりやすく説明すると・・・
- ステップ1
- 電気量を持たない導体が存在
- 導体から無限に離れた場所を電位の基準として、そこにNこの電荷(電気素量eを持つ)
- 電荷を1個運んで導体につける
- 導体は電荷eを持ち、基準点について電位がV(e)となる。
- この時の位置エネルギーはeV(e)
- ステップ2
- 電荷をもう一つ運んで導体につける
- 導体は電荷2eを持ち、基準点について電位がV(2e)になる
- この時の位置エネルギーはeV(2e)

区分求積法の記事はこちらですが、見比べてみると・・・




コメント