こんにちは。Horyです。
今までにコンデンサの様々な問題に取り組んできました。
今回の記事ではコンデンサ内に極板がある問題の攻略に関する記事を書きたいと思います。
よく出る問題なので必ず解けるようになりたいモノですね。
問題 コンデンサ内に極板
以下に示すのはコンデンサ内に極板がある場合の問題の攻略です。

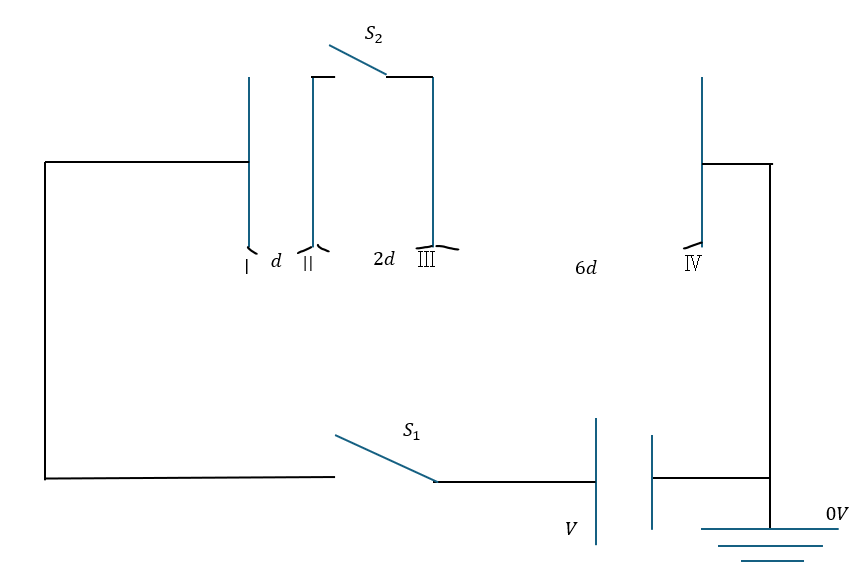
この問題を例に取り組みます。(2)の操作を変えたときの違いに気づけるかどうかが鍵ですね。
(1)解答・解説
ひとまず、極板における電場と電気量を以下のように定義します。
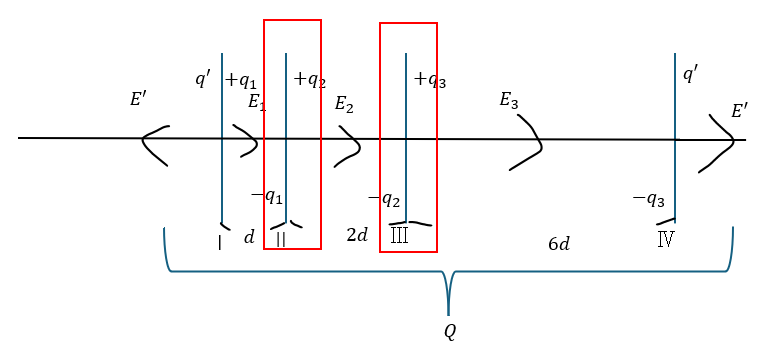
ポイントは以下の通りです。
- S1を閉じる・・・アースする⇔電荷は0⇔q’=0
- 孤立した部分の電気量は保存する
孤立した部分の電荷量が0で保存することを利用します。
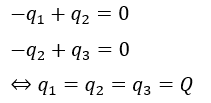
また、極板間の電荷を以下のように描くことができます。
今回はq1とq2,q3の電気量が全て同じ値なので・・・
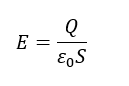
極板間の電場はこの値で一定です。
回路の方程式で。このコンデンサの電位差はVのため・・・
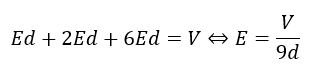
以上により、電位は・・・
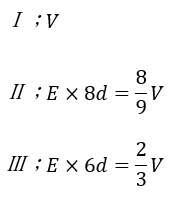
(2)-(ⅰ)解答・解説
この問題ですが、解説を3段階に分けます。
- S1を閉じる
- S1を開く
- S2を閉じる
この3段階に分けます。
S1を閉じる
S1を閉じると言うことは(1)と同じ状況になることです。
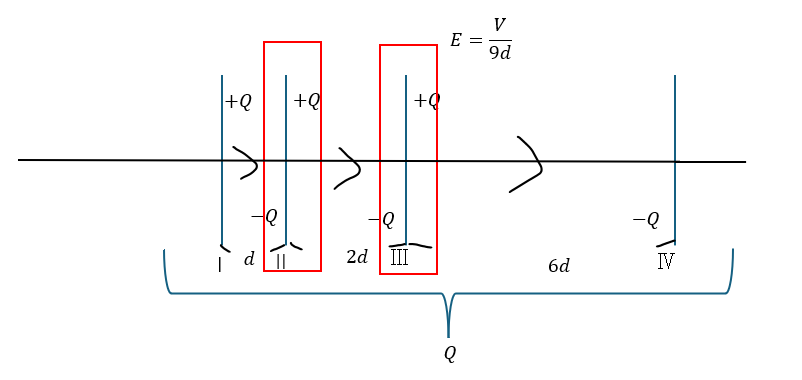
まぁ、これは解いたので分かりますよね。
S1を開く
次に、S1を開きます。
開いたと言うことは、回路図を考えると極板Ⅰ自体が孤立系になります。だから、極板Ⅰの左右の電荷は保存されます。
ただ、孤立系になっただけなので全体の状態については(1)と不変です。
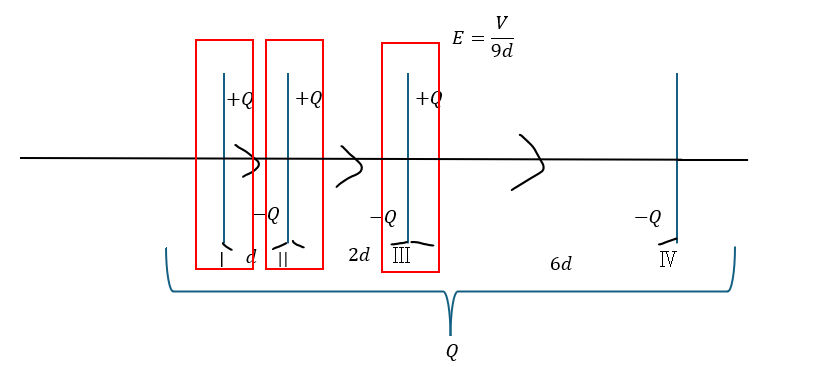
S2を閉じる
次にS2を閉じると言うことは、極板2と極板3の間は導線で繋がるので電気を貯めることはできません。
(正電荷と負電荷が流入→相殺して電気量が0になる)
ただし、極板ⅡとⅢは共に孤立しているので電気量は0で保存されます。
ただ、S1は開いたママなので電場 (コンデンサ内の電束=電気力線の数)は変化することはありません。
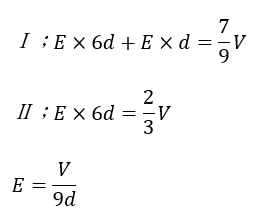
(2)-(ⅱ)解答・解説
この問題ですが、解説を2段階に分けます。
- S1を閉じる
- S2を閉じる
S1を閉じる
S1を閉じると言うことは(1)と同じ状況になることです。

まぁ、これは解いたので分かりますよね。
S2を閉じる
次に、S2を閉じます。
閉じたと言うことは、極板2と3が導線で繋がれた状態なので極板間に電荷はたまりません。
ただし、S1が閉じたママなので、このコンデンサの電位差自体はVになります。
何が起こったかというと、極板の厚みが小さくなったけど、電位差は変化しないので極板間の電場が強くなった(電束=電気力線の数が増えたことになります。
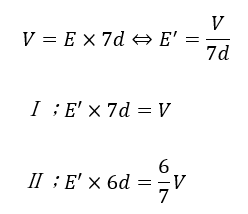
(3)解答・解説
まず、絶対に勘違いしてほしくない点としてこれは直列接続したコンデンサではありません。
コンデンサの中に極板が入っているだけです。ただ、それぞれのコンデンサの左右に電荷がたまっているので・・・
- 極板1と2間・・・コンデンサ
- 極板3と4間・・・コンデンサ
- 極板2と3の間に電荷はない・・・コンデンサではない
のようになって、コンデンサの中にコンデンサがあるみたいな状態になっています。
ⅰの場合
まぁ、電気容量の式に当てはめて、それぞれの極板間の電位差を求めます。
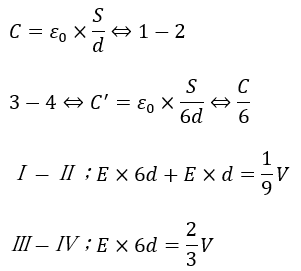
以上により、それぞれのコンデンサのエネルギーの和を考えると・・・
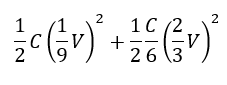
ⅱの場合
まぁ、電気容量の式に当てはめて、それぞれの極板間の電位差を求めます。ただ、ⅰのときと電場の強さが違うことに注意です。
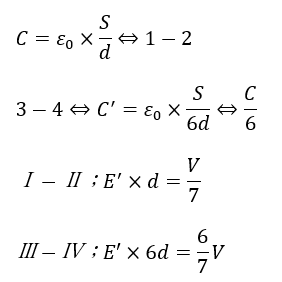
以上により、それぞれのコンデンサのエネルギーの和を考えると・・・
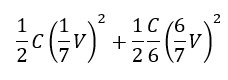


コメント