こんにちは。Horyです。
前回までにコンデンサの様々な問題に取り組んできました。
今回の記事では変わった形のコンデンサの問題に取り組みます。
正直、コンデンサを作るのであれば、平板コンデンサが一番楽です。
ナノで、今回紹介するコンデンサは社会で余り使われていない(マイナー)のモノが多いです。ただ、それも遊び心というモノなので、今回も頑張りましょう。
はじめに・・・
コンデンサの問題にたくさん取り組んできたと思いますが、基本的に手順は以下の通りです。
- ①ガウスの法則で極板内の電場を求める
- ②求めた電場で電位差を求める
- ③電位差と電気量から電気容量求める
- ④蓄えられるエネルギーを求める
ちなみに、電位差を求める時に、「V=Ed」の公式を丸暗記することだけはやめてくださいね。
電位や電場の定義は散々言ってきたと思いますが・・・
- 電場・・・電気量Qの電荷から+1Cの単位電荷が受ける力
- 電位・・・無限遠から無限の時間を掛けてやってくる+1Cの単位電荷がクーロン力にされる仕事
- 位置エネルギー・・・保存力と微小変位ベクトルの内積の線積分
電位は+1Cの電荷がクーロン力(保存力)によりされる位置エネルギーです。
問題1 導体球に電荷を貯める
以下に示すのは導体球に電荷を貯めるためる問題です。

この問題を例に解説します。当たり前のようにガウスの法則を用いますのでまだの人は以下の記事を読んでおいてください。
導体球の表面に貯めるというのがポイントです。
問題1 解答・解説
電場を求めるためにガウスの法則を使います。
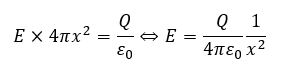
ここで、微小電荷dQを無限遠方から導体球の表面まで運ぶのに必要な仕事をクーロン力から考えます。
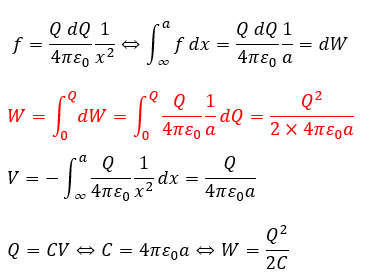
赤い部分で答えは出ています。この球はコンデンサではないので上に出てくるCは電気容量ではないただの定数と思ってください。
問題2 円板型のコンデンサ
次の問題は普通なら平板のコンデンサが円板で配置されている問題です。

まぁ、別に難しくない問題です。ガウスの法則で求める時の面積が円の面積になっただけですから・・・
問題2 解答・解説
まぁ、まずはガウスの法則で電場を求めます。
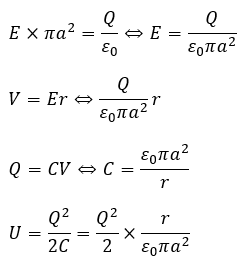
問題3 円柱に穴が空いたコンデンサ
次に示すのは円柱に穴が空いたコンデンサの問題についてです。

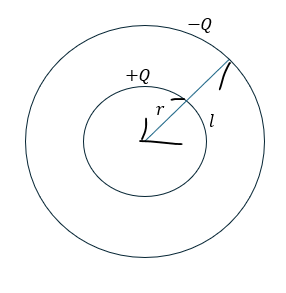
問題3 解答・解説
問題3の解答・解説です。
まずは、ガウスの法則で電場を求めます。これは、円柱の電場を求める時と同じ方法で求めます。円柱の高さが不明ですが、適当にhと設定します。
ここで、重要なのが、今回はコンデンサの問題です。
容量を求めるので、内径と外径の電位差を求めレバ良いです。だから、内径-外径間の電場を求めれば良いです。
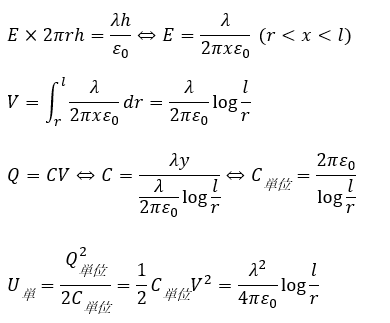
問題4 球型のコンデンサの電気容量
以下に示すのは球型のコンデンサの容量を求める問題です。

この問題を例に解説します。
問題4 解答・解説
問題4の解答・解説です。
基本的に「ガウスの法則→電場→電位差→容量」です。
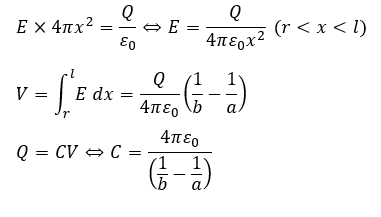



コメント