こんにちは。Horyです。
前回の記事ではコンデンサの原理を解説すると共に、コンデンサが社会のどのようなところで応用されているかを学びました。
今回の記事では、コンデンサの外側の電場が0になる理由を問題と共に解説します。
今回も頑張りましょう。
問題 コンデンサ
以下に示すのは今回取り組む問題です。

向かい合わせてコンデンサを作ったときの状況を図に示します。
電場の方向とかは分かっていると思いますが、今回は分からないことを前提として問題を解きます。
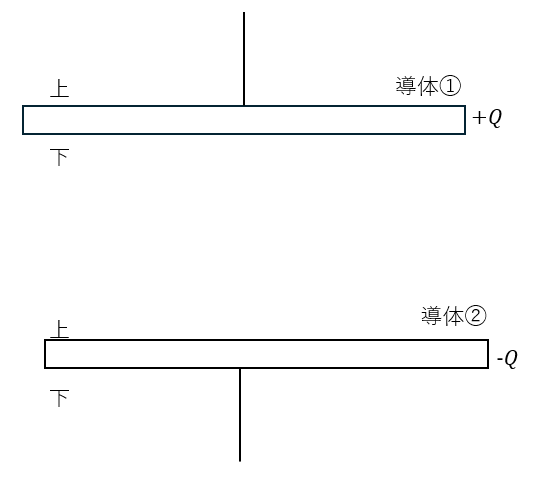
(1)解答・解説
まずは、図を描いてみます。
ただ、これは前回の記事でもやった内容なので復習程度で頑張りましょう。
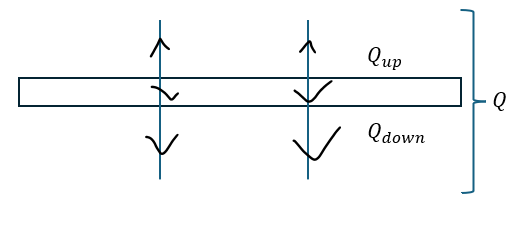
ここで、電荷が極板の表面にしか分布しないので導体内の電場は0になります。
未知量であるQupとQdownを求めれば良いです。
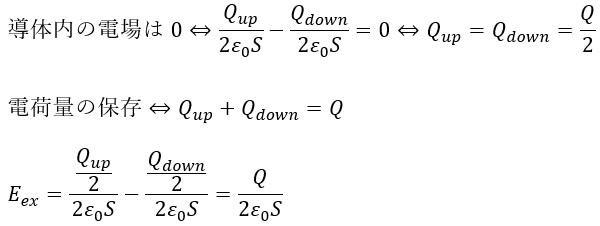
(2)解答・解説
こちらの問題は少々面倒ですが、まずは、図を描いてみます。
この問題が今回の記事で一番大事な問題です。
なんでコンデンサの外側の電場は考えなくて良いのか(コンデンサは内側だけに電荷がたまるのかが分かります)
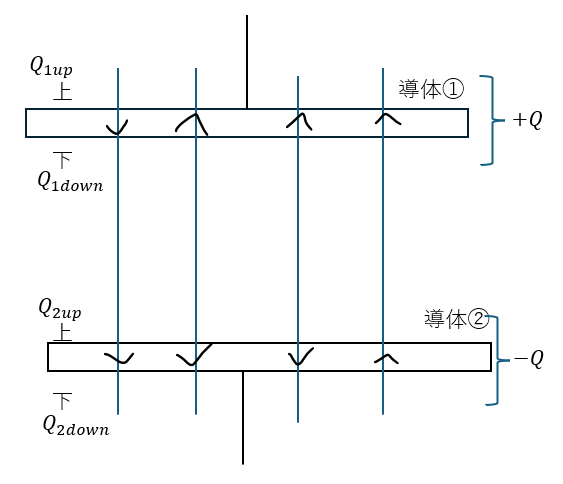
導体①と②での電場の和は0になります。
- Q1up・・・導体1で下向き・導体2で下向きの電場
- Q1down・・・導体1で上向き・導体2で下向きの電場
- Q2up・・・導体1で上向き・導体2で下向きの電場
- Q2down・・・導体1で上向き・導体2で上向きの電場
「仮に」、4つの電荷が上の向きを向く電場を出していると考えます。何故、このように非対称的に式を立てるかは後で説明します。

①+②と②-①を実行します。
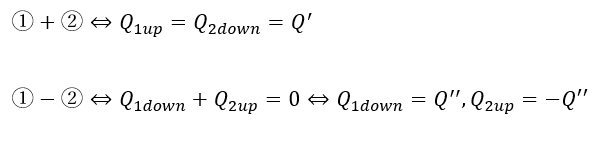
これで、それぞれの極板の上下の具体的な電荷量は分からないですが、関係性を把握することはできました。突破口を見つけました。
このコンデンサの合計電荷量が0デあることを利用します。つまり・・・
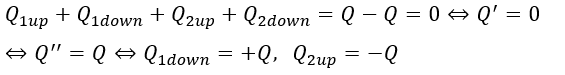
コンデンサの外側の電荷量が0になることが分かりました。
だから、前回の記事でコンデンサの電場を求める時は、外側の電場を考えずに内側の電場だけ考えたのですね!
余談・・・
導体中での電場の向きを以下のように対称的に定義した場合、困ったことが起こります。
- Q1up・・・導体1で下向き・導体2で上向きの電場
- Q1down・・・導体1で上向き・導体2で下向きの電場
- Q2up・・・導体1で上向き・導体2で下向きの電場
- Q2down・・・導体1で下向き・導体2で上向きの電場
これで式を立てた場合①+②と①-②は0になってしまうため話が始まりません。
(3)は前回散々やったので自習してください。


