こんにちは。Horyです。
前回の記事では導体と誘電体の違いについて簡単に解説すると共に、両者を電場の中に投入した際の電化の動き方の違いも説明しました。
今回の記事ではこれを応用したコンデンサの原理を解説すると共に、コンデンサが日常のどのような所に応用されているかを簡単に解説します。
理学と工学の違い
コンデンサについて簡単に解説する前に、理学と工学の違いを説明します。
どちらも自然科学(数学・物理・化学・生物)を扱うことは共通していますが・・・
- 理学・・・原理や法則を用いて真理を突き詰めよう
- 工学・・・原理や法則を応用して社会の役に立てよう
上に示した違いがあります。
高校の電磁気学では理学と工学は以下のように分けられます。
- 電磁気・・・理学
- 電気回路・・・工学
コンデンサは電気回路で出る内容です。そのため、この記事の内容は工学に関する物になります。ただ、工学にも理学の知識は必要です。
コンデンサとは・・・
まず、コンデンサとは簡単に説明すると、「導体板を向かい合わせて作った装置」になります。
また、コンデンサの役割は簡単に説明すると「電気を貯めること」です。
これが社会のどこで使われているかというと、スマホやパソコン・車など様々なモノに使われています。
というのも、スマホやパソコンは電気で動きますが、電流が流れすぎると当然壊れてしまいます。
コンデンサは電気を貯めることで、機器に大電流が流れて壊れないようにする役割があります。
だから、コンデンサは私たちの生活になくてはならないモノです。
余談ですが、電気回路などの工学分野を勉強するなら、機械や装置が社会のどんなところで役立っているかを学ばないと意味がないと思います。
コンデンサの原理
コンデンサの原理を解説します。
導体を2つ用意して向かい合わせで配置します。導体①と②があるとして、①の負電荷を②に移すとします。
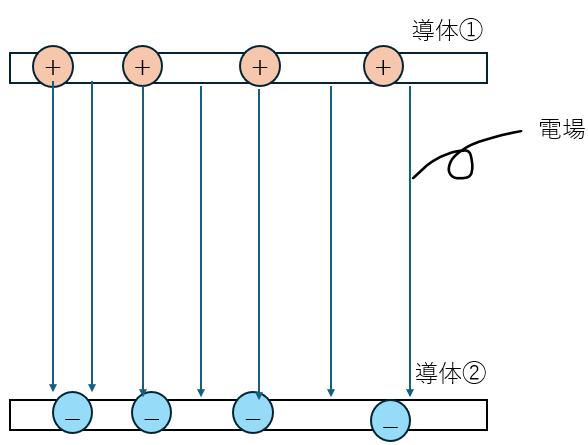
上図に示すようにコンデンサ内には上下方向に電場が発生します。
電場の大きさをガウスの法則を使って求めてみましょう
(図には正電荷と負電荷がそれぞれ4つしかないが実際は無数にある)。
ガウスの法則についてはこちらの記事です。
コンデンサと電場
ガウスの法則を用いてコンデンサの電場を求めてみます。
導体①と導体②で一旦、分けて考えます。電場の向きについては電場の定義を思い出してください。
電場の定義は「+1Cの電荷が受けるクーロン力」と見なせます。
ここで、導体板の面積をSとします。電場の大きさを求めます。
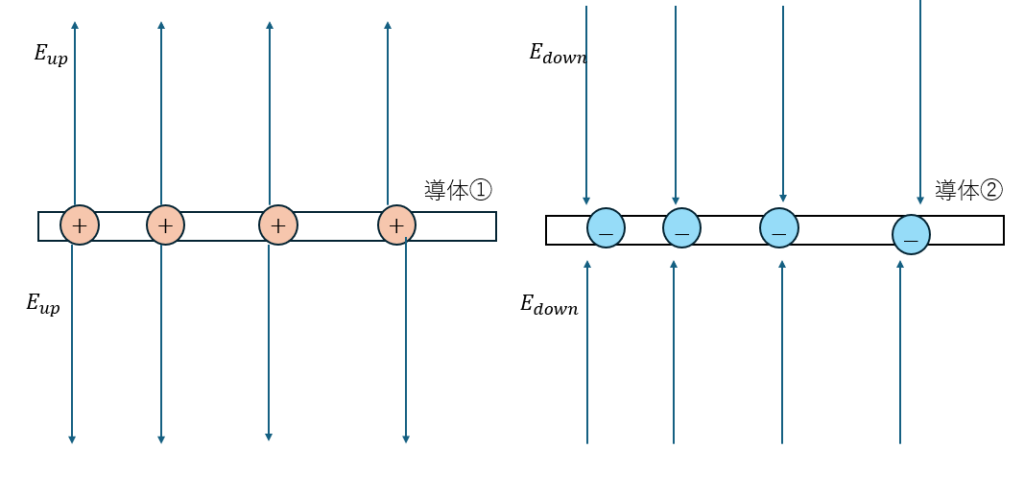
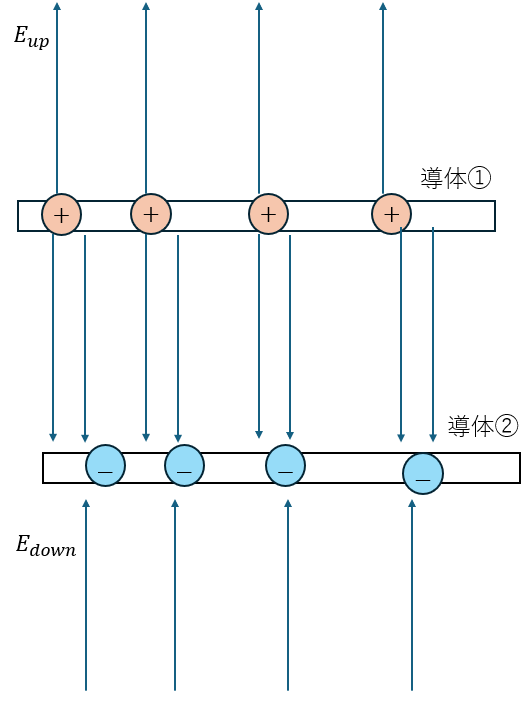
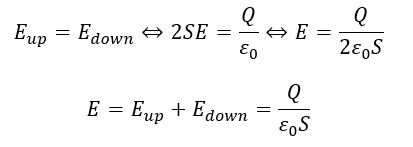
コンデンサ内部の電場は導体①と②においても下向きです。
コンデンサの電位と電気容量
コンデンサに関して導体①と②の間の電位差を求めてみます。
電位を定義通りに求めます。ただし、導体間の距離をdとします。
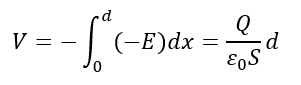
そして、電気容量Cは以下のように表せます。
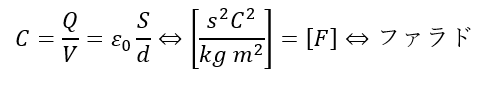
コンデンサのエネルギー
コンデンサの位置エネルギーを考えます。ただし、2つの方法があります。
- 方法①;極板自体を運ぶ
- 方法②;電荷を運ぶ
この中で電荷を運ぶという方法は「連続近似体」という難しい方法を用いないとできません。
要は、位置で積分するのではなく、電気量自体で積分する方法です。
今回は②の方法を用います。
導体板①を導体板②の位置まで運ぶことを考えます。
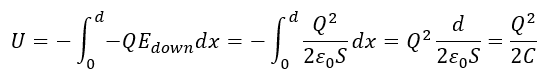
コンデンサと誘電体
コンデンサの極板間を誘電体で満たした場合を考えてみましょう。
以下に図を示します。
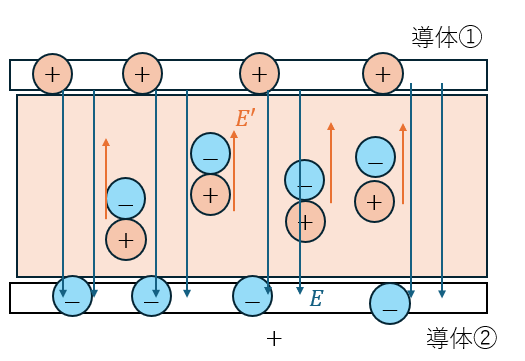
誘電体内の電場の大きさは以下のように求められます。
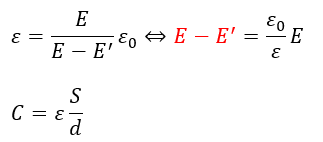
電場の求め方は前回の記事でやったので復習しておいてください。



コメント