こんにちは。Horyです。
前回の記事では表面や内部に一様に電荷が分布している場合の電場や電位を求めました。
ただ、電荷が分布するのは球だけではありません。
棒や平面にも電荷は分布して電場は発生します。今回は棒(円柱)や平面に電荷が分布したときの電場・電位を求めていこうと思います。
もちろん、ガウスの法則を用いるのでこちらの記事は読んでおいてください。
棒や円柱・平面は対称性があります。電場勾配が一定ならガウスの法則で簡単に電場が求めれます。
今回も頑張りましょう。
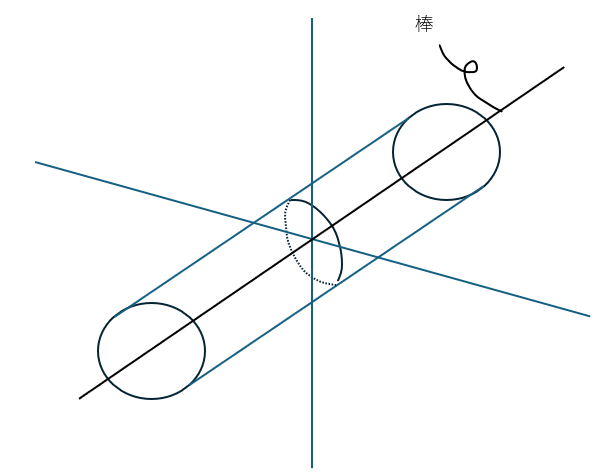
問題1 無限の長さを持つ棒の電場
以下に示すのは無限の長さを持つ棒が電荷を持つときの電場を求める問題です。

問題1 解答・解説
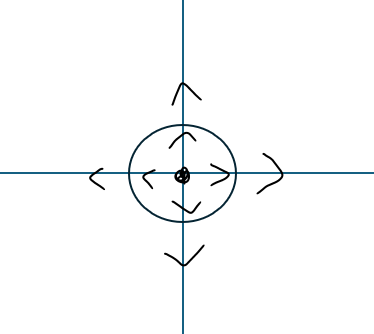
今回は側面の電場を求めれば良いです。
この円柱を金太郎飴のように切ることで断面を見ます。
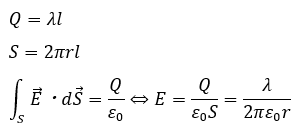
以上が解答になります。
問題2 無限の広さを持つ平面の電場
以下に示すのは無限の面積をもつ平面が電荷を持つときの電場を求める問題です。

この問題を例に解説します。まずは、図を示します。
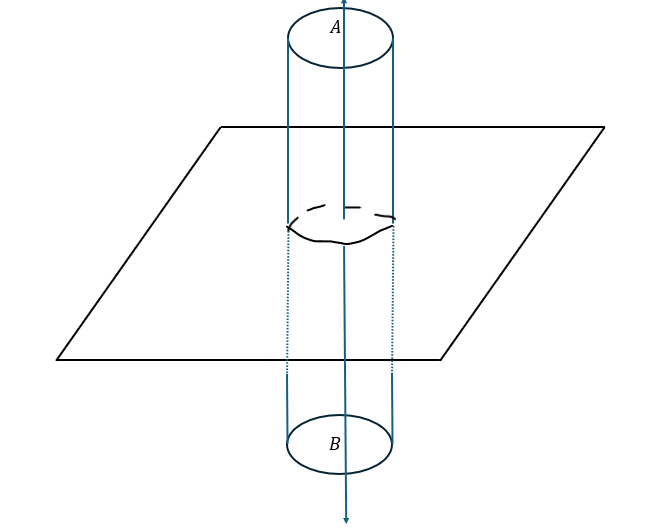
問題2 解答・解説
まずは、面上の電荷を求めると共に、ガウスの法則でこの平面が放出する全電気力線の本数を求めます。
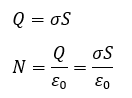
これによって平面が出す全電気力線の本数は求めれました。
今回は平面で上側と下側で分かれるので、上側A・下側Bのそれぞれの本数は半分のN/2になります。
これをガウスの法則に応用して・・・
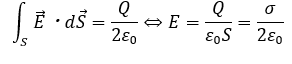
以上が解答になります。
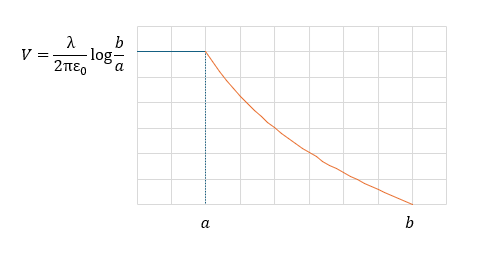
問題3 無限に長い円柱に分布する電荷による電位分布
以下に示すのは無限に長い円柱の表面に分布する電荷による電位分布の問題です。

以下に図を示します。
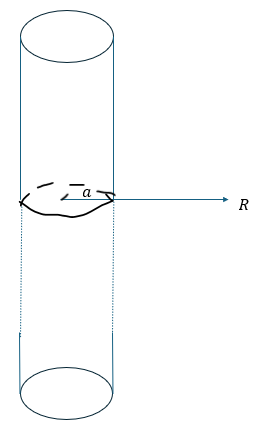
- (ⅰ)r=bでの電位を0とせよ
- (ⅱ)r=aでの電位を0とせよ
円柱の表面に電荷が分布
まずは、ガウスの法則で電場を求めます。また、この問題では電位の基準点は無限遠方上ではなく、r=bの地点です。
- 円柱内部・・・電場は0
- 円柱の外側・・・電場あり
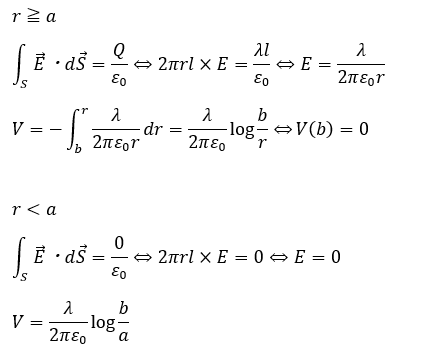
円柱全体(内部にも)に電荷が分布
問題4の解答・解説です。まずは、ガウスの法則により電場を求めます。
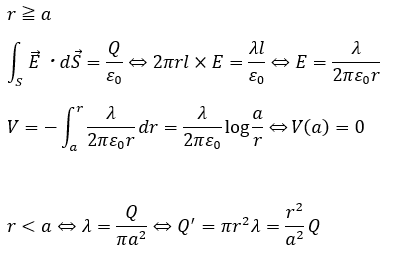
ここで、求めているのは円柱の半径がr(<a)になったときの電気量です。まぁ、円柱の断面積を考えれば電気量が上のようになることも分かると思います。
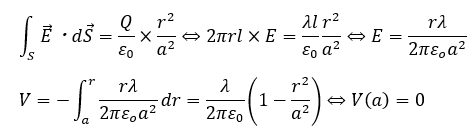
グラフは自分で書いてみてください。


