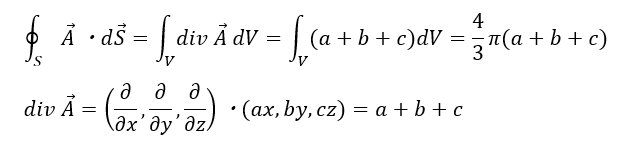こんにちは。Horyです。
前回の記事までは点電荷のおけるクーロン力から電場や電位について簡単に解説しました。
また、これらに関する問題も攻略しました。
ところで、前回の記事で電気力線について解説したと思いますが、立体の表面を貫く電気力線の本数や、大きさ・広がりを持つ電気量を持った物体が出す電場などを求めてみたいですよね。
そんなときに使える法則がガウスの法則です。
今回の記事ではガウスの法則について解説します。電磁気学における超重要法則の1つなので必ず理解したいです。
今回も頑張りましょう。
ガウスの法則
そもそも、ガウスの法則とは以下のような式のことを言います。
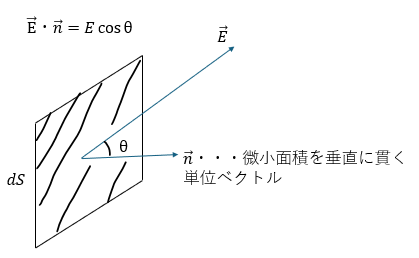
ただし、任意の立体の表面積をSとし、体積をVとします。また、電場の大きさをEとします。
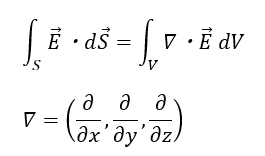
微分演算子についてはこちらの記事に書いてあるので読んでおいてください。
また、立体は任意で良いですが、今回は分かりやすくするために立方体を考えます。

- 積分の中身;微小面積dSを通る垂直方向の電場の量
- 全体の意味;表面積Sの立体を通って外に出る電場(ベクトル)の量
- 要は・・・立体の表面から湧き出す量
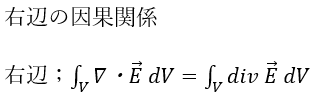
- 積分の中身;div・・・単位体積から全方向に湧き出す量
- 積分の中身;div (vec E) dV・・・微小体積から電場(ベクトル)が湧き出る量
- 全体の意味;体積Vの立体から湧き出る電場の量
ちょっと分かりやすいように立方体での図を示します。
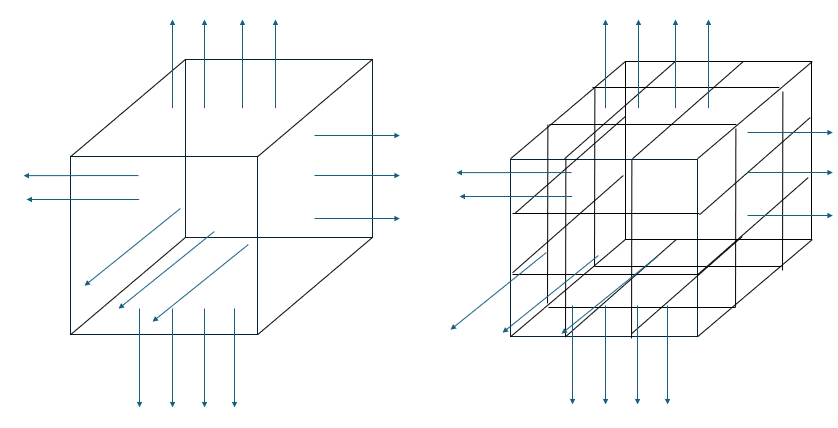
- 左辺・・・立体の表面から湧き出す電場(ベクトル)の量
- 右辺・・・立体の内部から湧き出る電場(ベクトル)の量
- 意味・・・「湧き出る」量と「湧き出す」量は等しい
考えてみれば当たり前のことですがこれがガウスの法則であり、このことを証明します。
ガウスの法則の証明
ガウスの定理を証明します。この証明は2段階に分かれます。
- 一段階目・・・左辺について考える
- 二段階目・・・一段階目を利用して右辺を考える
一段階目
左辺について考えます。
以下のような立体を貫く電場を考えます。
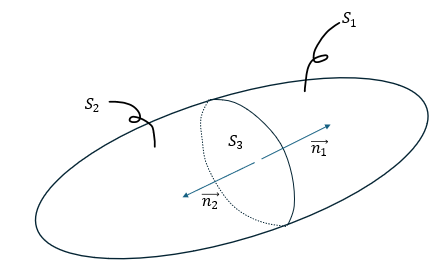
ここで、S1側から湧き出る量とS2側から湧き出る量を考えます。
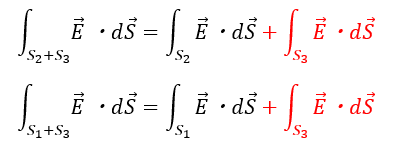
上の式を合算させれば良いですが、同じ面のベクトルで向きが真逆で大きさも同じのベクトルは打ち消し合います。なので、赤い部分は消えます。
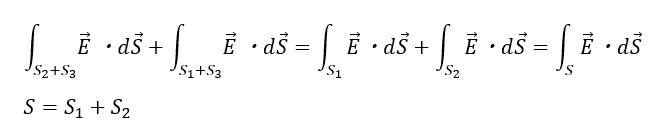
二段階目
二段階目です。本来、ガウスの法則は立体がどのような形であっても成立しますが、今回は簡単のために、立方体を考えます。
面の名称をSiとします(i=1,2,3,4,5,6)。
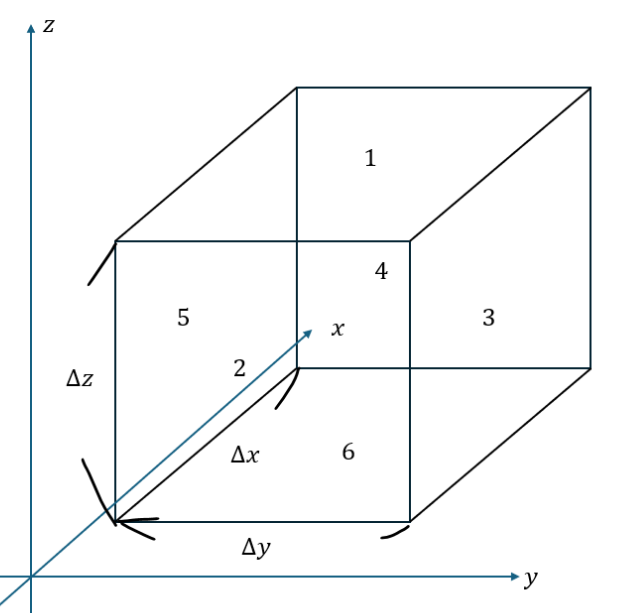
ここで、この立方体表面から湧き出す電場の量を考えると・・・
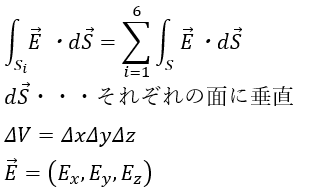
ここで、上面と下面のS1とS6を考えます。また、3次元空間座標を考えます。
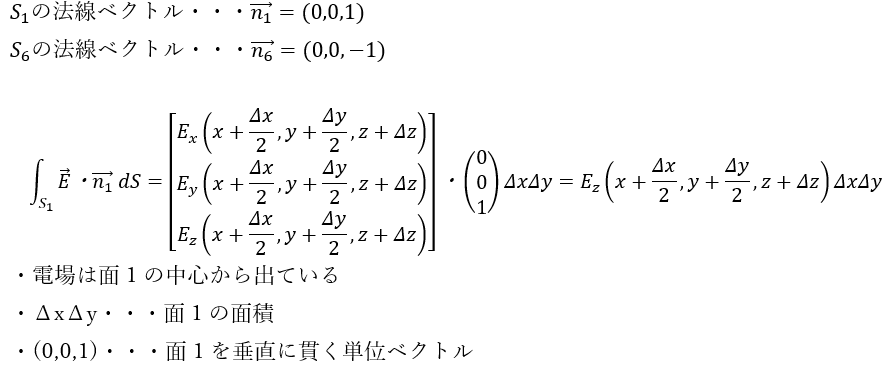
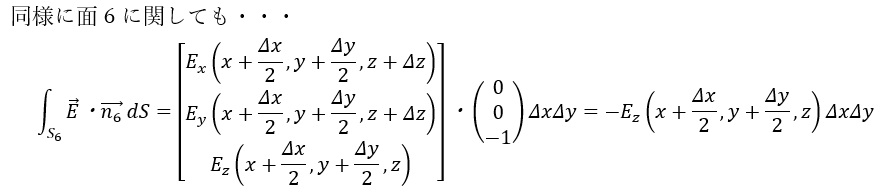
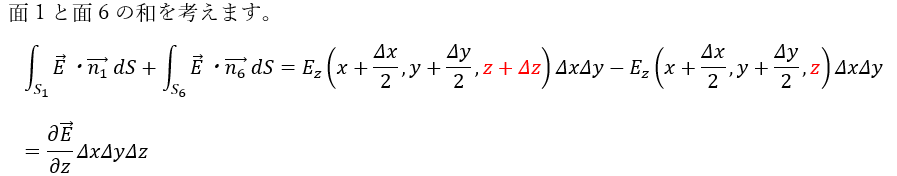
引き算でz成分が微小成分になることがポイントです。だから、偏微分で表せます。
同様の方法を用いると「面3と面5」・「面2と面4」についても・・・
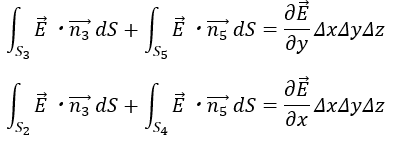
よって面1から面6から出て行く電場の量を全て足し合わせます。
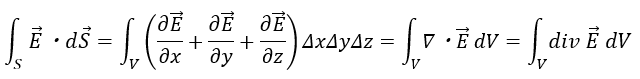
よってガウスの法則は成立します。
ガウスの法則 問題1
ガウスの法則を用いた簡単な問題をやってみましょう。

ちなみに、ガウスの定理と法則の違いですが・・・
- ガウスの定理・・・数学的なベクトルの湧き出し (数学)
- ガウスの法則・・・ガウスの定理のベクトルが電場に (物理)
問題1 解答・解説
問題1の解答・解説になります。
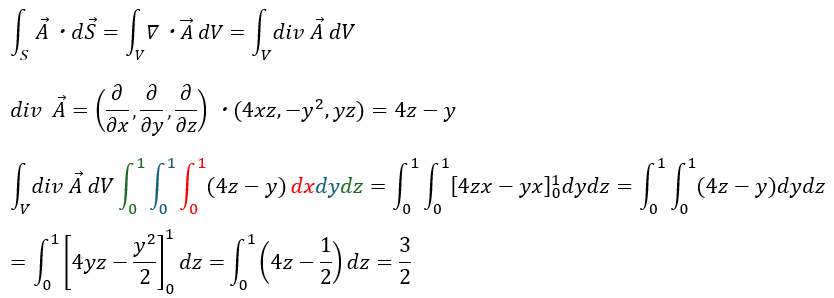
この積分を多重積分と呼びますが、恐れることはありません。
内側から順次処理すれば良いだけです。
ガウスの法則 問題2
続いてはガウスの法則の問題2です。

上の積分記号に丸をつけたモノは周回積分と呼ばれ、円周に沿って積分するとき・球面に沿って積分するとき等に使います。覚えといてもいいかもです。
問題2 解答・解説