こんにちは。Horyです。
前回の記事ではクーロン力についての定義を確認すると共に、クーロン力を利用して電荷は発生させる電場と電位について説明しました。
今回の記事ではこれらに関する問題に取り組みます。
今回も頑張りましょう。
前回の復習
前回の復習を行います。
ただ、前回とは違う方法を用います。
座標平面上でクーロン力を考えて運動方程式を作ることでエネルギー保存則を導出し、そこから考える方法を用います。
以下のような状況を考えます。ただし、2つの点電荷の電気量の符号は同じと考えます。
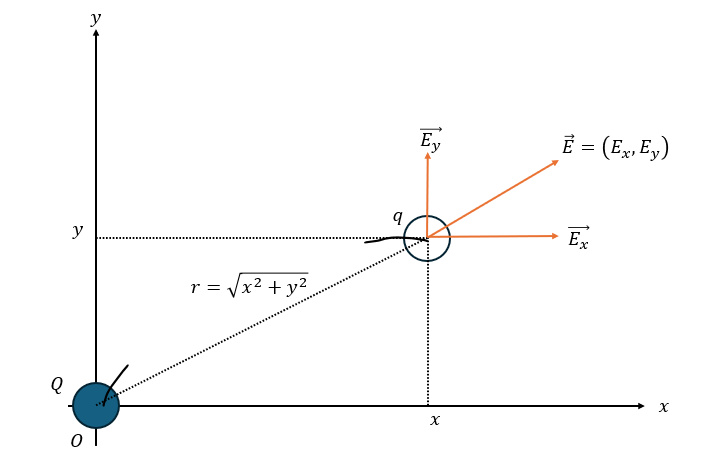
ここで、電場(ベクトル)と大きさを考えます。動径方向(中心から離れる方向)を正とします。また、電場を成分ごとに分解します。
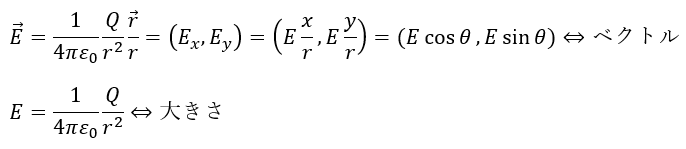
上に書いた電場は原点にある点電荷 (電気量Q)が出している電場です。
点(x,y)にある質量mの電荷が受けるクーロン力を考えて電気量qをもつ点電荷の運動方程式を記述します。
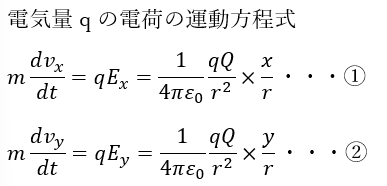
ここで、エネルギー保存則を考えます。「①×vx+②×vy」の演算を行います。
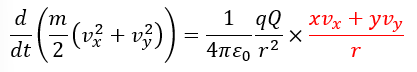
ここで、電気量qを持つ点電荷について、位置(x,y)をtで微分します。
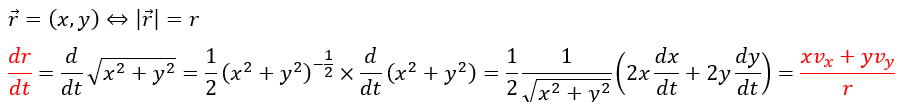
ここで、上の式を利用すると共に、運動エネルギーを以下のように設定します。
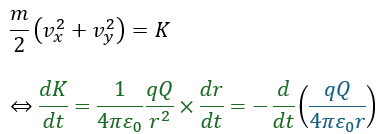
上の緑の式がエネルギー保存則の式で、その式内の青い部分がクーロン力による位置エネルギーと呼ばれるモノです。
また、この式で電位は以下のように定義できます。
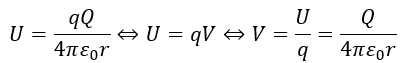
ここまでは前回の内容です。一応、単位について前回の記事で解説します。
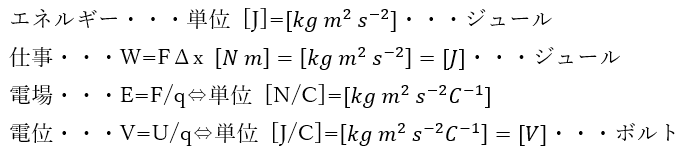
- 電場はベクトル量
- 電位はスカラー量
問題1 点電荷と電場の成分と電位のグラフ
以下に示すのは点電荷と電場の成分を求める問題です。比較的に簡単な問題なのでこれは解けるようになってほしいです。

この問題を例に解説します。まずは、図を描いてみます。
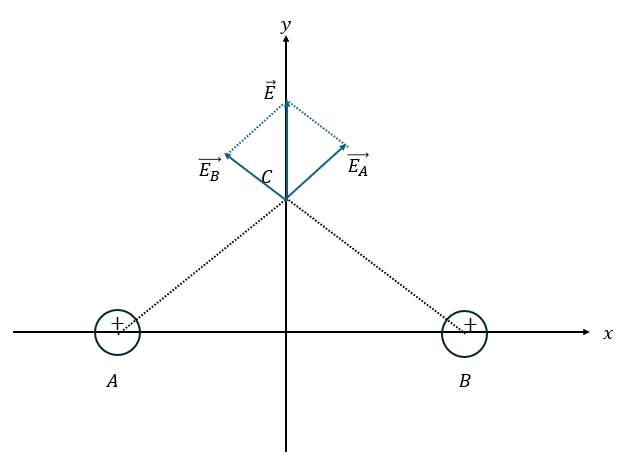
- 電場・・・電場はベクトル⇔ベクトル的な足し算
- 電位・・・電位はスカラー⇔スカラー的足し算 (普通の足し算)
- 電荷の配置はy軸に対称的
- 電場は「+1Cが受ける力」⇔クーロン力は斥力⇔電場の方向
問題1 解答・解説
問題1の解答・解説です。
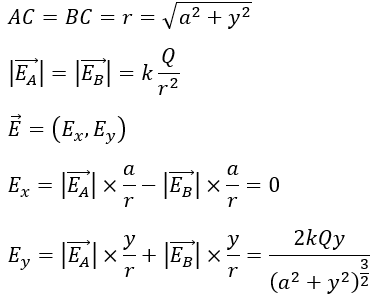
以上により成分を計算することができました。
X方向の電場は対称的な場合、打ち消しあいます。Y方向の電場のみ考えれば良いです(ベクトル的な足し算に気をつけてください)。
続いて、電位についてデス。電位はスカラー的足し算です。
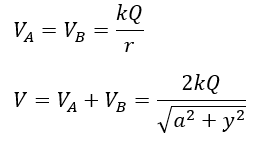
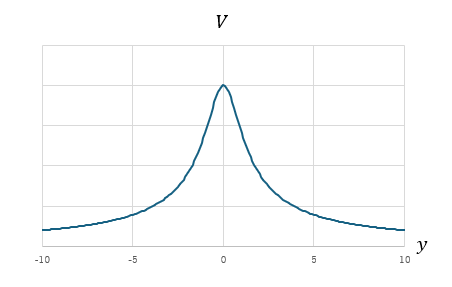
問題2 電荷とエネルギー保存則
続いては、電荷とエネルギー保存則に関する問題です。

この問題を例に解説します。まずは、図を示します。
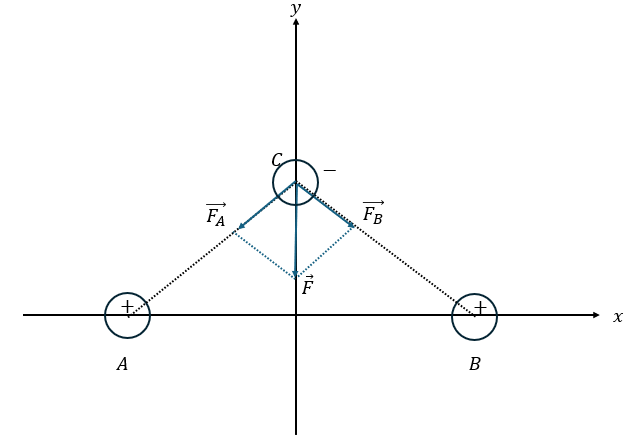
電荷は異符号なので、引力になります。
力をベクトル的に合成すると、x軸方向の力は打ち消しあってy軸方向の力が残ります。だから、y軸の負の向きに運動します。
問題2 解答・解説
無限遠での速度とクーロン力の位置エネルギーは0になります。
なので、仮に戻らないとして、点Cでの力学的エネルギーと無限遠(x=0∩y=∞)での力学的エネルギーは保存します。
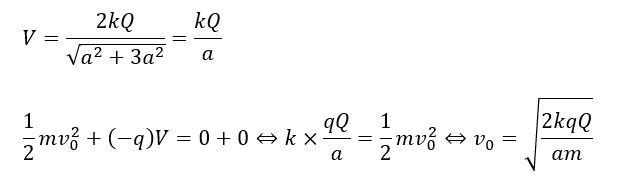
戻ってこないようにする条件を考えます。(y→∞でv→v∞)になると仮定します。
Cに戻らないなら、無限遠方で電荷の速さが正になれば良いです(要は戻ってこないようにする)。
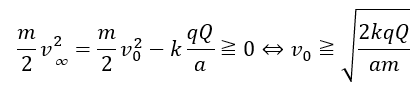
問題3 クーロン力と単振動
点電荷の配置は問題1と同じにする。

この問題を例に解説します。まず、図を示します。

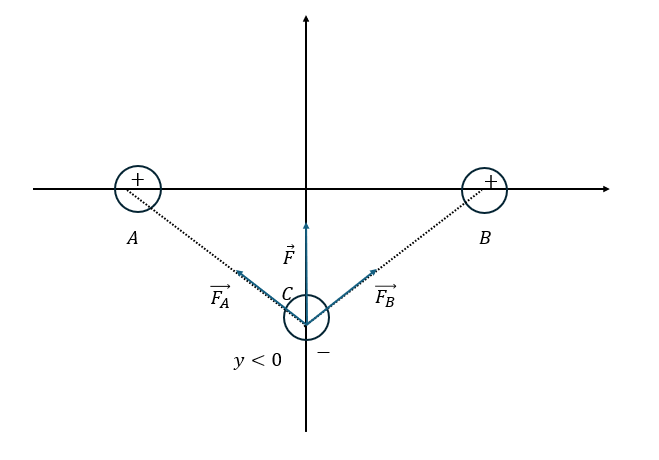
今回は初速度が与えられてません(静かに離すから)。
また、クーロン力が引力で、力の向きを考えると・・・
- 電荷の位置がy>0・・・力の向きはy軸の負の方向
- 電荷の位置がy<0・・・力の向きはy軸の正の方向
これらを考えると確かに単振動を行うことが分かります。
問題3 解答・解説
まずは、電荷の運動方程式を作ります。
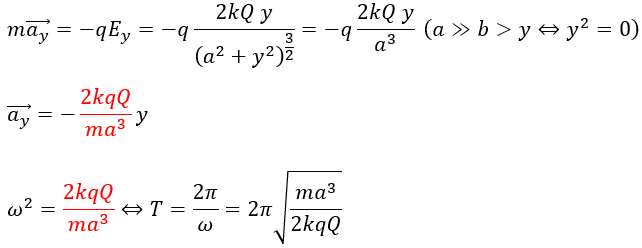
今回は周期を求めるだけなのでこれで終わりです。運動を記述して議論するならば微分方程式を解かないといけません。



コメント