こんにちは。Horyです。
前回の記事で電磁気学の導入を解説すると共に大学内容になりますが、場の概念とベクトル演算子について解説しました。
今回の記事では、クーロン力について解説すると共に、クーロン力が電場や電位とどういう関係があるかを紐解いていきたいと思います。
今回も頑張りましょう。
点電荷とクーロン力
最初にクーロン力についてです。
大きさを無視できる2つの点が電荷を持っているとします。これを点電荷といいます。
点電荷が持つ電荷をQ1,Q2とおくと2つの電荷間に「働く力の大きさ」は次の式で表せます。
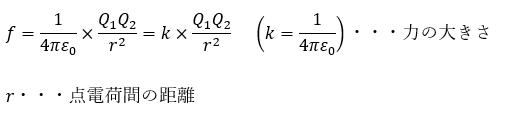
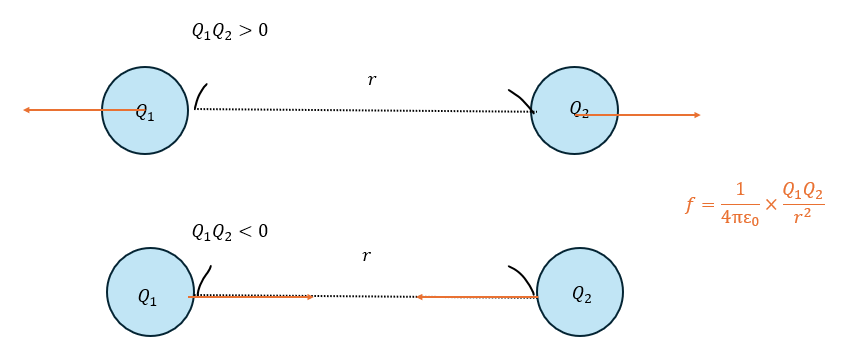
- 2つの電荷の符号が同じ・・・Q1×Q2>0⇔斥力 (反発する向き)
- 2つの電荷の符号が違う・・・Q1×Q2<0⇔引力 (引き合う向き)
この力の大きさ・向きの条件などを全て含めて「クーロンの法則」と言います。
以下に図を示します。
静電場の定義
静電場とは、静止した電荷が発生させる場の一種で、定義としては、「単位電気量+1[C]当たりに働くクーロン力」のことです。
なので、電場の大きさはクーロン力を用いて以下のように書けます。
(ベクトル表示でなくてスカラー表示されていることに注意してください。)
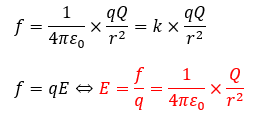
上の赤い部分で書いた式が点電荷1つが出す電場の大きさの式です。
この式の意味は、点Pでの電場の大きさがEで、その点Pにやがてやってくる電気量qの粒子がやがて「f=qE」の大きさの力を受けるという意味です。
ベクトルで表してみると・・・

当たり前ですが、電場はベクトルなので、方向は電気量の正負に依存します。
ただし、注意してほしいのが、上のことが言えるのは大きさが無視できる点電荷の場合に限り言うことができます。
- 点電荷・・・クーロンの法則⇔電場・電位の定義
- 球面を貫く電気力線の本数⇔ガウスの法則 (また今度)
- 大きさ・広がり持つ物体が電気量持つ・・・ガウスの法則⇔電場・電位の定義 (また今度)
電場の描き方について・・・
電場の定義について、先ほど説明したことをおさらいします。
点電荷1つが出す電場は以下のように書けました。

- 電場は点電荷の周囲の点に無数にできる
- 点電荷から距離が遠ざかるほど電荷の大きさは小さくなる
電場を真面目に描くと以下のように描けます。
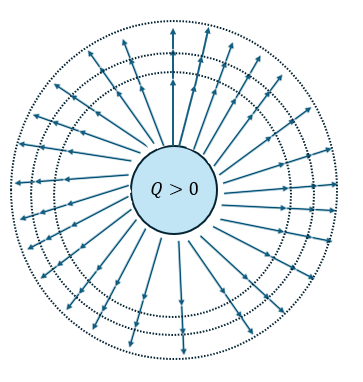
図に示すのはQ>0の時です(Q<0なら中心に向かう方向)。
図にはたくさん書いてありますが、実際は細かいのが無限にあってとてもじゃないですが書き切れません。
だから、代表的なものだけを書けば良いです(地図の方位と同じ、東西南北しか書かない)。
以下に代表的な電場だけを書きます。
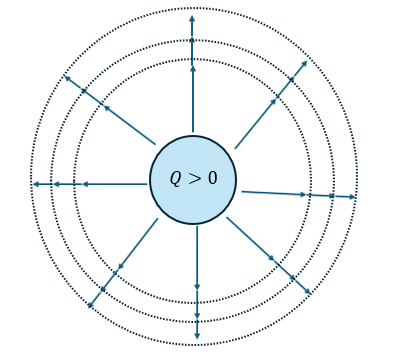
まぁ、電場を描けと言われたら8方位ぐらいで描けば十分だと思います。
- 電場の矢印を繋げたもの・・・電気力線
- 磁場の矢印を繋げたもの・・・磁力線
クーロン力による位置エネルギー
前回の記事でも説明しましたが、クーロン力は保存力です。
なので、クーロン力による仕事は位置エネルギーになります。
位置エネルギーとか仕事の話は力学の記事でも紹介しましたので読んでおいてください。
(力学ができないと電磁気学も理解できません。)
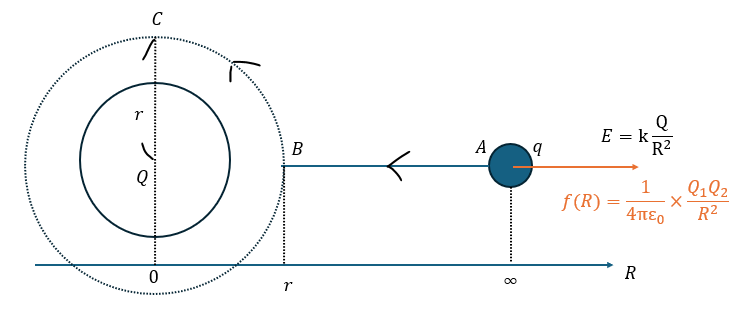
以下のようにA→B→Cのようなルートをたどるときのクーロン力の位置エネルギーを求めます。
基準点を無限遠方とします(無限遠方で位置エネルギーが0)。
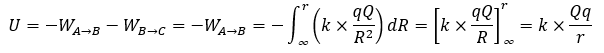
電位の定義
電位の定義は単位電気量当たり(+1[C])に働く位置エネルギーのことです。
だから、電位はスカラー量で大きさのみを持っています
かみ砕いて説明すると、無限遠方上の点Aの+1Cの点電荷をA→B(C)まで運んだときの位置エネルギーのことです。
つまり・・・点B (C)での電位をVcとすると・・・
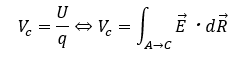
電荷が1つだけの場合を考えると・・・
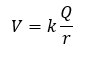
点電荷1つの電場と電位について・・・

- 青い矢印を結んだ線・・・電気力線
- 点線の円・・・等電位面 (同心円状で電位の大きさは同じ)
次回から点電荷についての練習問題です。
頑張りましょう。



コメント