こんにちは。Horyです。
今回の記事では3次元における円柱座標と直交座標の極座標変換に関して話します。
二次元の極座標に関しては数学の記事でも話したので必要であれば読んでおいてください。
この分野ですが、円柱極座標は比較的に簡単と思います。
ちなみに、今回の記事は大学内容です。
今回も頑張りましょう。
3次元円柱座標
3次元円柱座標に関して話します。
直交座標に対して3次元円柱座標は以下の図に示すように取ります。
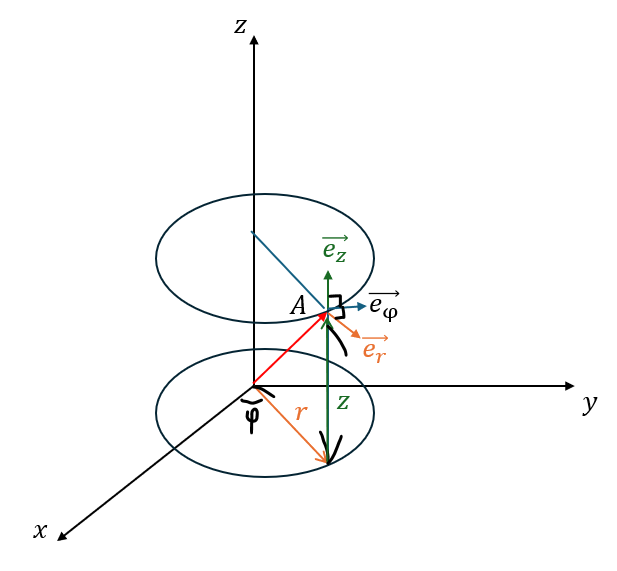
直交座標に対する3次元円柱座標です。
eベクトルは3次元円柱座標における単位ベクトルになります。
単位ベクトルとは大きさが1のベクトルのことです。直交座標は以下のように表せます。
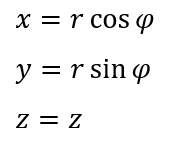
上のように考えると、3次元円柱座標も所詮は二次元極座標を拡張したモノだと分かります。
点Aの位置ベクトル
点Aの位置ベクトルを求めてみます。これはベクトル的足し算になります。
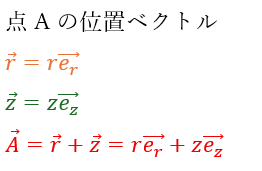
円柱極座標→直交座標
次に円柱極座標を直交座標で表してみます。
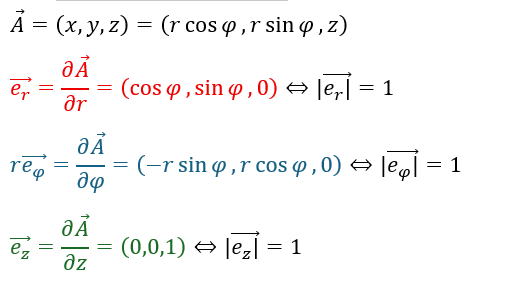
単位ベクトルの直交
円柱極座標の各単位ベクトルが直交していることを示します。
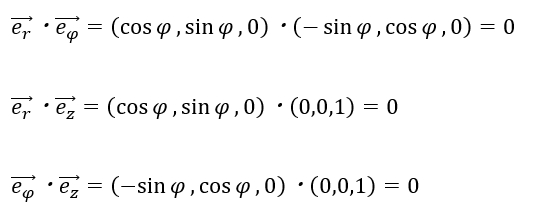
ベクトルの内積が0なので確かに単位ベクトルは互いに直交しています。
速度ベクトル
- 速度ベクトル・・・位置ベクトルを時間で一回微分した量
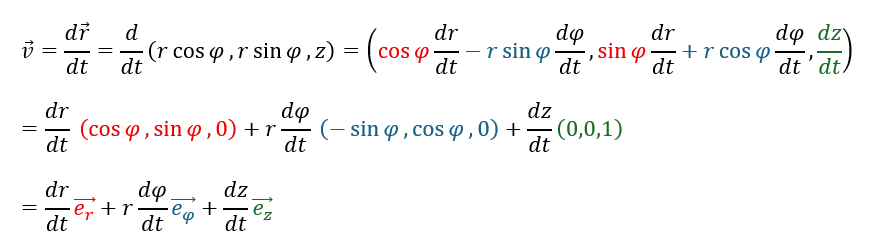
加速度ベクトル
- 加速度ベクトル・・・位置ベクトルを時間で二回微分した量
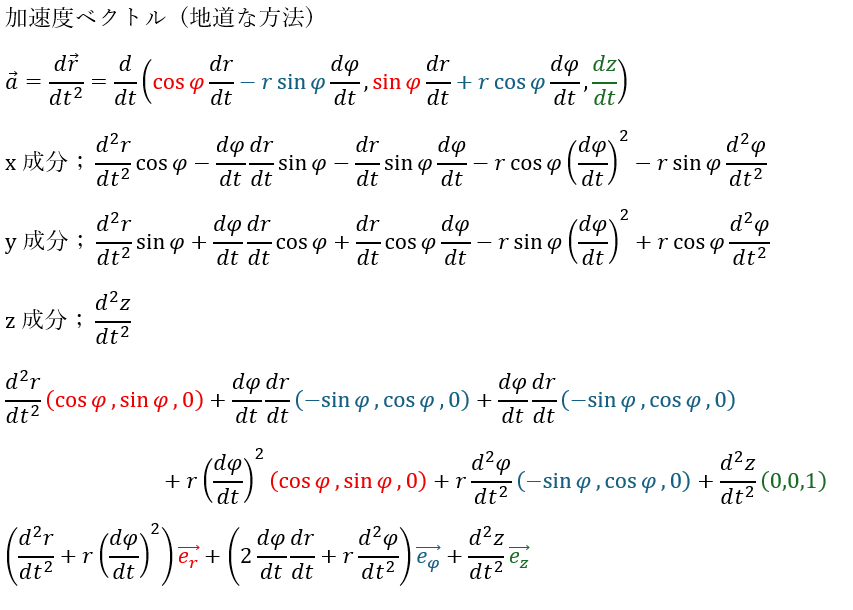
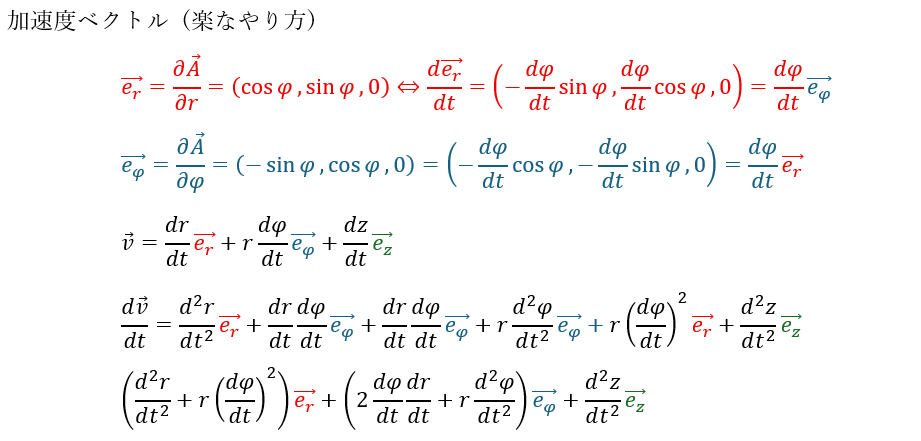
加速度ベクトルは楽なやり方でも地道なやり方でもどちらでも出来るようにしてください。
理系の学問は基本的に計算を行う学問です。
この程度の計算でへこたれていてはいけません(大学ではこの程度の計算は普通に出てきます)。



コメント