こんにちは。Horyです。
今回の記事では3つの自然数について、2数の和を残りの数で割った余りが1になる問題について解説します。
本問は整数問題で範囲の絞り込みを行う良い問題です。
今回も頑張りましょう。
本記事で取り組む問題
以下に示すのは本記事で取り組む問題になります。

この問題を例に解説を進めていきます。
まずは、問題を解く前に準備をします。

このまま直接的に3数を求めようとしても文字が6個もあるので無理そうです。
そのため、商についての条件から範囲を絞り込んでいきます。
ただし、変形に色々と工夫をします。
工夫については3数の大小関係を使えそうです。
難しい問題に見えますが本質的には以下の記事で紹介した問題と全く同じです。
ステップは以下の通りです。
- まずは、①と②の商を特定する (数値が小さい方の商から優先的に特定)
- 商を求めて①と②に代入して変形
- yとzをxのみで表す
- 最後に③をxの式で表してxを特定→yとzの特定
商の特定
まずは、商の特定から行います。
①の式を変形させます。
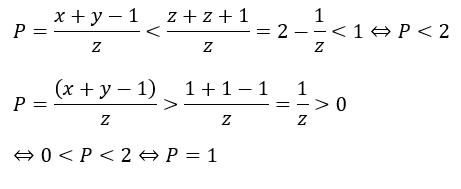
ひとまず、Pが1と分かったので式①を書きなおします。
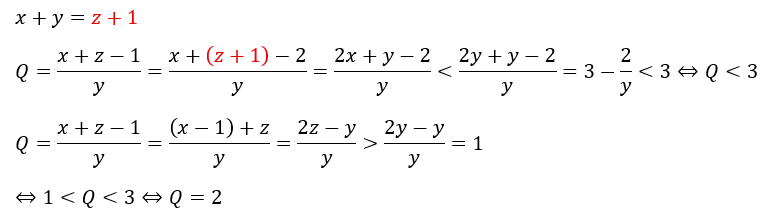
これによりQも2であることを特定できました。
自然数の特定
自然数の特定を行います。
ひとまず、Q=2と分かったので②の式へ代入します。ここで、P=1を代入させて①を変形させた式も用いれば、、、
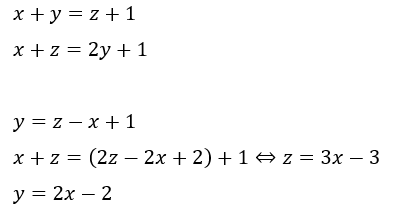
これにより、y,zを1つの文字で表すことができました。
これらを式③に代入します。
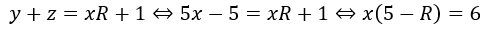
これは整数問題の定石の一つである積の形になります。約数×約数で解決します。
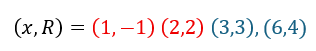
上の式の赤いものは不適切です。何故なら、x=yとなって大小関係が成立しないからです。
青いものが適切な数値で・・・
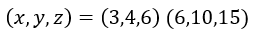
以上により数の特定ができました。


コメント