こんにちは。Horyです。
皆さんは二次関数の問題や二次方程式の問題に取り組むことが良くあると思います。
それらの問題で出てくる関数や方程式の数は1つか2つぐらいかと思います。
二次方程式が3つ出る問題とか無理やろ!と思うかもしれませんが、入試ではそんな問題も出てくるかもしれません。
今回の記事では二次方程式が3つ出てくる問題について、「実数解」をテーマにした考察を行おうと思います。
今回も頑張りましょう。
3つの二次方程式
以下に示す3つの二次方程式に関して考えます。

これらの3つの二次方程式に関して考察をしていこうと思います。
考察前の準備
考察前に下準備を行っていきます。
3つの方程式をみて思うことは係数のp,q,rが①~③の式で均等であることです。
そして、皆さんは不等式の決まりを覚えていますでしょうか?
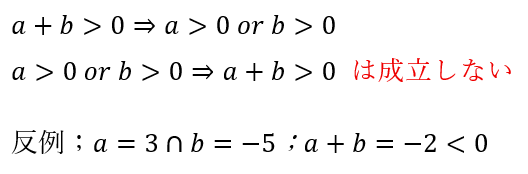
上のことを応用すると・・・

これを用いて二次方程式で遊んでいきます。
考察①;判別式の和
上の3つの二次方程式の判別式を設定します。

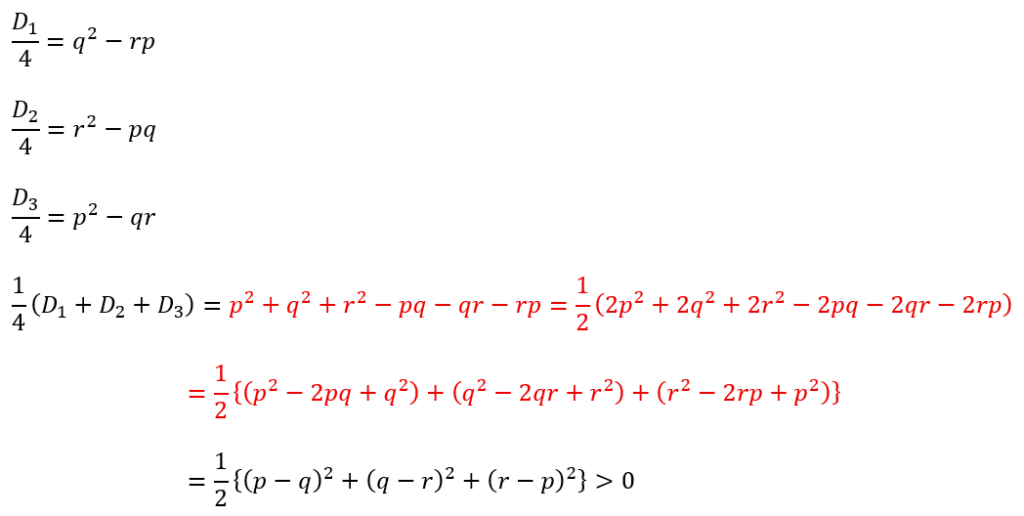
上の式の赤い部分の変形は記憶に値する価値があります。
0より大きい理由はp,q,rが異なる実数だからです。
0より大きいことにより・・・
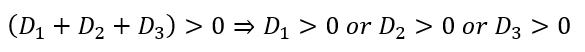
以上のことから上の3つの二次方程式のうち少なくとも1つは異なる2つの実数解を持つことが考察できます。
考察①;背理法によるアプローチ
考察①の結果を受けて背理法によるアプローチを行ってみましょう。
3つの二次方程式が異なる実数解を持たないと仮定します。
よって、3つの判別式の値は全て0以下になります。
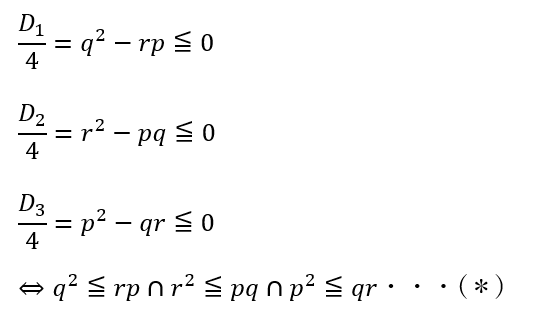
(*)の左辺は二乗の形になっていてp,q,rは0ではないです。
よって、左辺は必ず0より大きいです。従って、rp, pq, qrは0よりも大きいです。
ここで、(*)の辺々を掛けてみましょう。

これは、p,qが互いに異なっていることに矛盾します(前提条件との矛盾)。
よって、3つの二次方程式の内、少なくとも1つは異なる2つの実数解を持ちます。
考察②;共通解の存在
共通解の存在に関して考察をしていこうと思います。
共通解を持っていると仮定して議論を進めていきます。
理由としては「共通解がない」として議論を進めると非常にやりにくいからです。
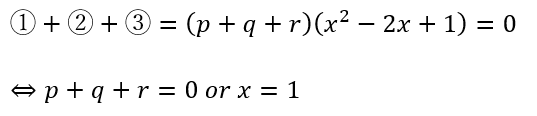
それぞれの場合について個別に解説します。
p+q+r=0
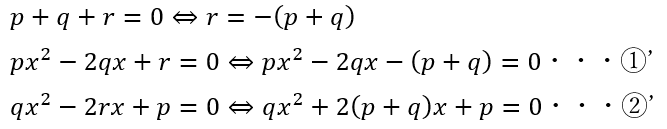
ここで、完成させた①’と②’で面白い事をしたいのですが次数を減らしたいです。
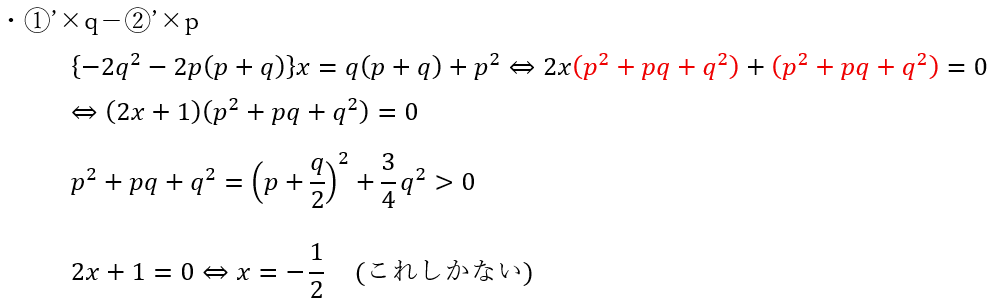
これしかないxを①’に代入してみます。
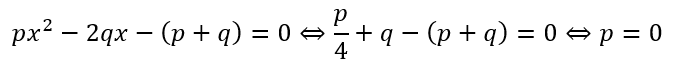
以上のことはpが0以外の実数であることに反します。
x=1
x=1の時を代入してみます。
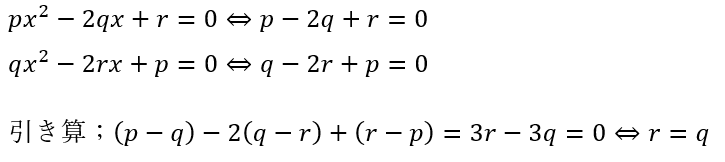
異なる実数であることに矛盾します。
考察②;結論
以上の事からどちらの場合においても共通解があると仮定して議論を進めた結果、矛盾が生じてしまうので3つの二次方程式は共通解を持ちません。
ちなみに、初めから次数下げを行う方法もありです。
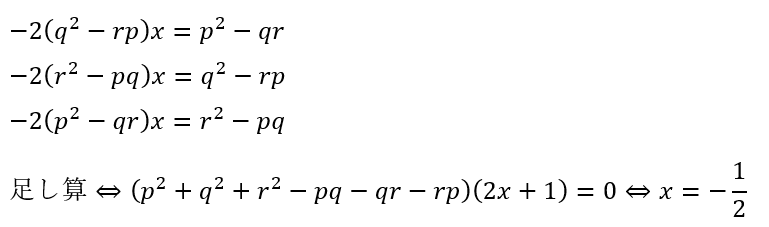
元の二次方程式のままでは対称性はありませんが、判別式になると対称性があるのが面白いですね。



コメント