こんにちは。Horyです。
以前に三角関数の記事で和関と積和の公式に関して話しました。
学生の多くは積⇒和ができますが和⇒積は圧倒的に出来ない印象を受けます。
そんな皆さんのために今回は積和を使う応用問題を紹介します。
今回も頑張りましょう。
問題;2つのsinの積と不等式
2つのsinの掛け算に関する不等式を証明します。
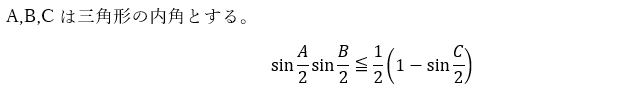
上の不等式を証明します。
やり方としては2つあります。
- 3文字⇒2文字 (右辺の変形)
- 積⇒和の利用 (左辺の変形)
解答方法を個別に紹介します。
3文字⇒2文字
文字を減らす方法を用います。
CをAとBで表して角を1つ減らします。
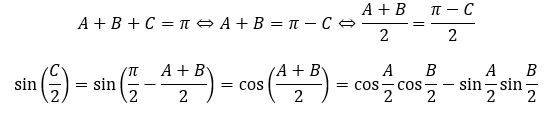
右辺に上の式を適用すると・・・

右辺から左辺を引きます。
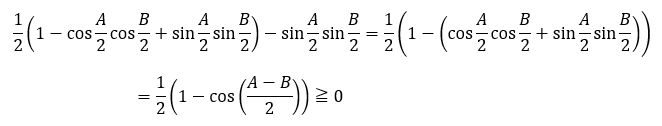
以上により不等式を示せました。
積⇒和の利用
左辺に積⇒和の公式を利用します。
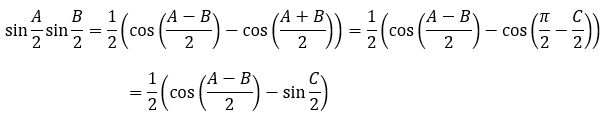
右辺から左辺を引きます。
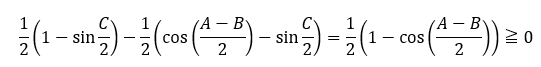
以上から不等式は成立します。
まとめ
「和⇒積」や「積⇒和」を利用する利点を自分なりにまとめると。。。
- 和か積のどちらかで統一したい (両辺とも同じ形にしたい)
- 和⇒積にすることで共通因数で括れる
- 和⇒積や積⇒和にすることで項が消える場合がアル
もちろん、半角公式や倍角公式を使うこともあります。
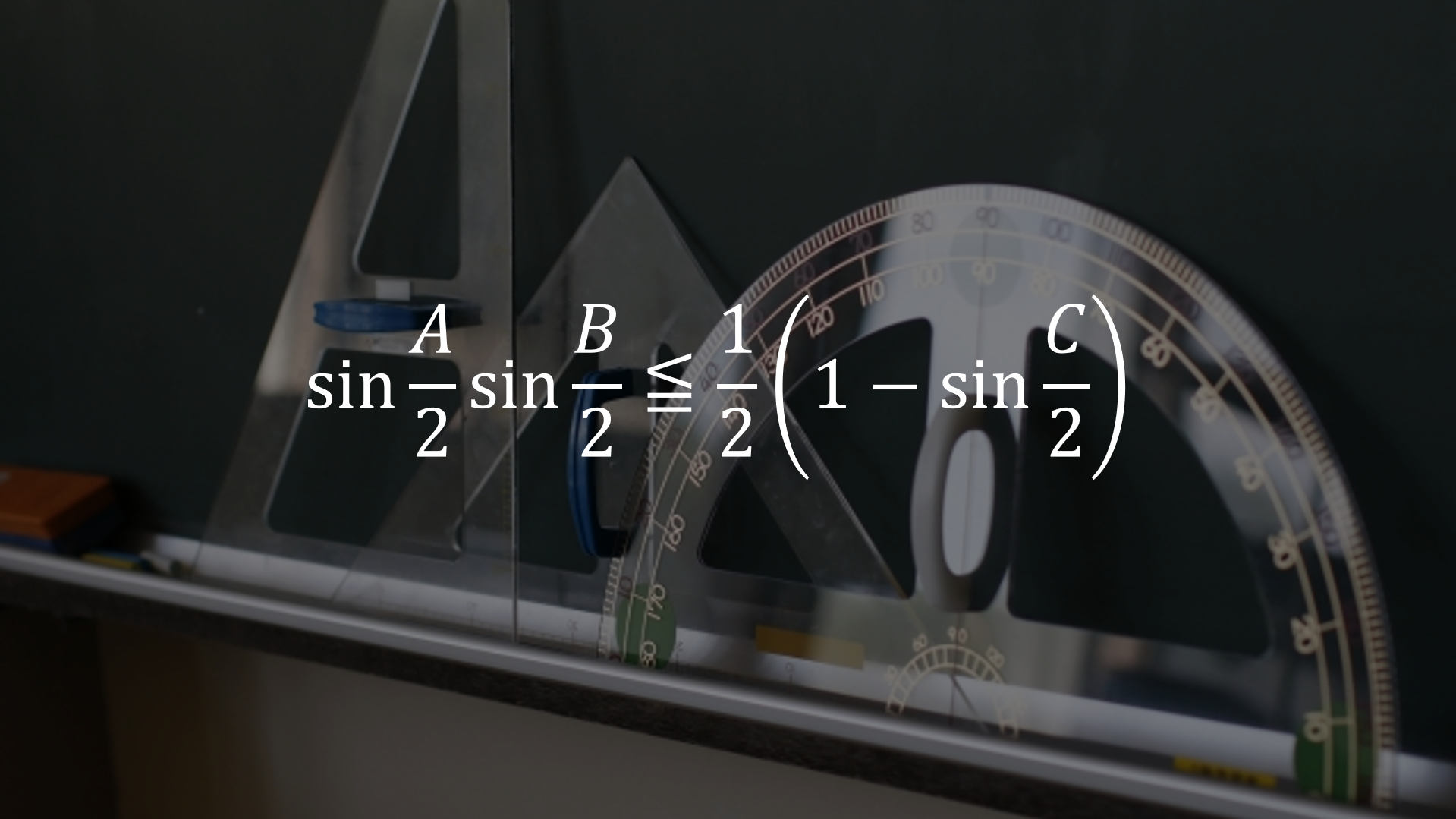


コメント