こんにちは。Horyです。
これまでに3次方程式に関しては学んで来たと思います。
3つの実数解に関して1つの解が他の2解の和になっていることがあります(この他にも等比数列になっている問題などもあるが・・・)。
今回はこの3次方程式の係数と解の特定に関して解説します。
今回も頑張りましょう。
1つの解が他の2解の和
以下に示すのは3次方程式に関する問題です。

この問題を例に解説します。
頑張りましょう。
問題を解く前の下準備
問題を解く前の下準備です。
pとqの関係が分からなければ無理そうなのでp,qの関係式を求めてみます。
3次方程式の解と係数の関係を用います。
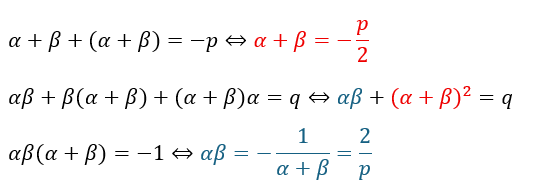
赤い部分と青い部分を真ん中の式に代入すればpとqの関係式を割り出せます。
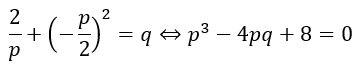
これによりpとqの関係式を割り出すことができました。
係数と解の特定
関係式が割り出せたので解と係数を特定します。
pとqは整数なので上の関係式は (約数)×(約数)の形にできます。
ここまで来たら整数問題の応用です。
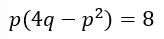
ここで、数学ができない奴はこのまま全ての約数を当てはめようとします。
絞り込みを使いましょう。
- 4q・・・qの偶奇に関わらず偶数
- pが偶数なら(4q-p^2)も偶数 (偶数-偶数)
- pが奇数なら(4q-p^2)も奇数 (偶数-奇数)
積が偶数でpと(4q-p^2)の偶奇が一致するので約数が1と8のように偶数と奇数で別れることはあり得ません。
よって、以下の4通りが考えられます。

それぞれの場合で解を考えます。
(p,q)=(-2,0)
数学ができない奴はこれをそのまま3次方程式に当てはめてゴリ押しで解を求めようとします。
α+βとαβが求まっているなら二次方程式を作れます。

以上からこの3次方程式は・・・
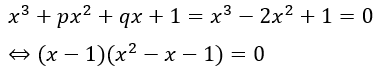
解については二次方程式の解の公式で自分で求めてみてください。
(p,q)=(2,2)
先ほどと同様の手法で求めます。

以上からこの3次方程式は・・・
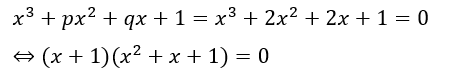
解については二次方程式の解の公式で自分で求めてみてください。



コメント