こんにちは。horyです。
前回の記事ではデータの分析で重要な要素である分散と標準偏差に関して学習しました。
今回の記事では2変量の関係を表すグラフとして散布図について解説するとともに、共分散や相関係数に関して解説しようと思います。
今回も頑張りましょう。
散布図について
散布図に関して解説します。
言葉で解説しても難しいので、例を挙げて解説します。
体力測定で10人のボール投げの飛距離[m]と握力[kg]を記録にとることを考えます。
- ボール投げの飛距離・・・x軸に対応
- 握力・・・y軸に対応
ボール投げの飛距離と握力の結果を10人についてまとめて記録を座標平面に対応させることでできるグラフを散布図といいます。
仮に以下の表に示すような測定結果が出たとすると・・・
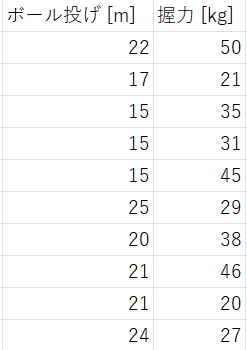
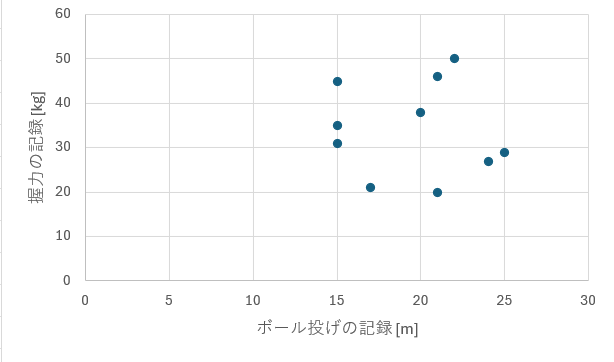
散布図は上の図に示すように表されます。
- 右上がりに分布・・・正の相関がある
- 右下がりに分布・・・負の相関がある
- 分布に傾向がない・・・相関関係なし
共分散と相関係数
共通テストで計算することはないと思いますが(計算してる時間はない)、共分散と相関係数に関して解説します。
出てくる文字に関しては以下のように考えます。

共分散は以下のような式で与えられる量です。
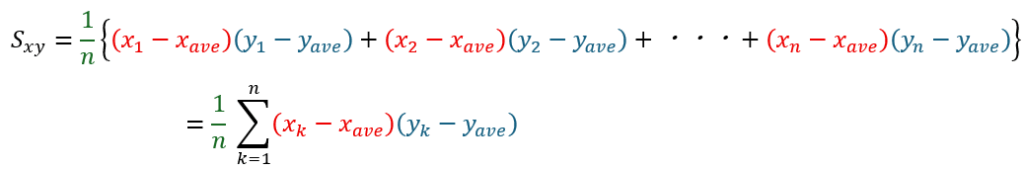
式だけで説明しても意味が分からないと思うので解説します。
- 赤い部分・・・xについて、各データの平均値との差 (負の値もあり)
- 青い部分・・・yについて、各データの平均値との差 (負の値もあり)
- 赤い部分×青い部分・・・長方形の面積 (負の値もあり)
- 緑の部分・・・長方形の和を平均化
ここで、グラフを用いて考えてみます。
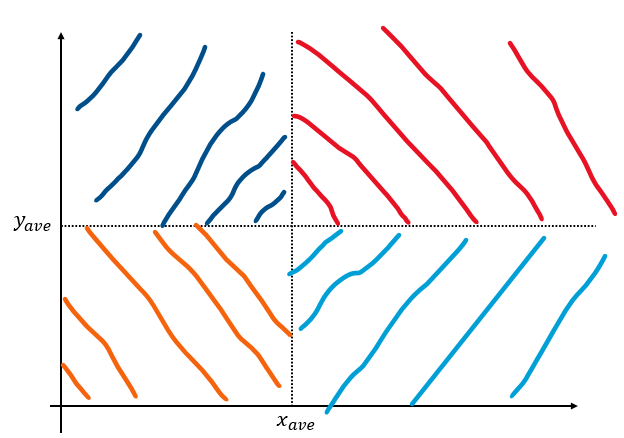
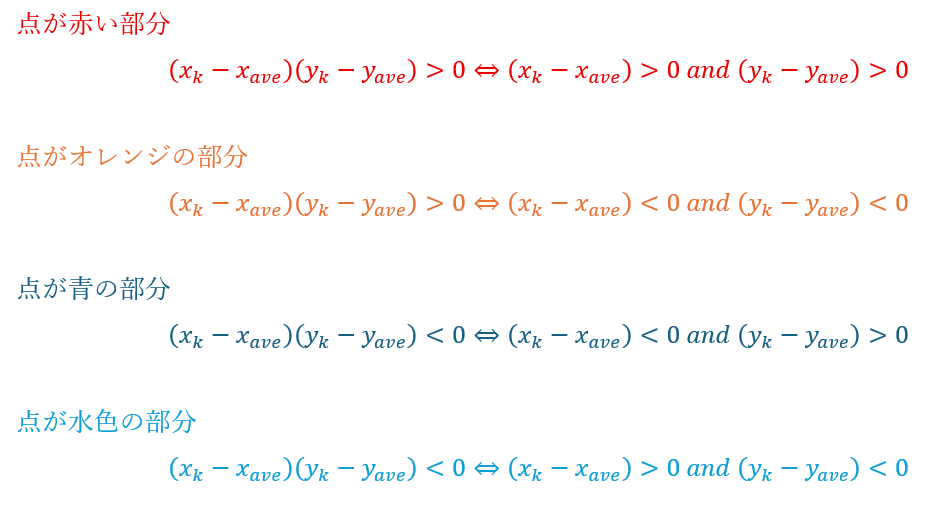
ここで、点が上に示した4つの部分の内のどこに集まることで、散布図がどんな相関を取るかを考えていただきたいです。
- 正の相関をとる⇔点が赤とオレンジの部分に集中
- 負の相関をとる⇔点が青と水色の部分に集中
相関係数は共分散とそれぞれの標準偏差を用いて以下のように定義されます。
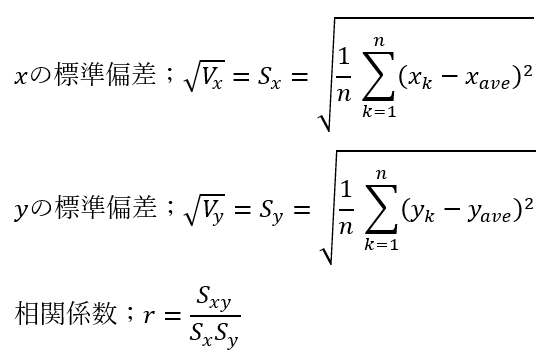
相関係数は共分散を標準偏差の積で割り算した量です。
標準偏差は必ず正になるので、相関係数の符号は共分散の符号と一致します。
- 相関係数 > 0 ⇔ 2辺量に正の相関関係
- 相関係数 < 0 ⇔ 2辺量に負の相関関係
- 相関係数 ≒0 ⇔ 相関関係はない
共分散;簡単な計算方法
共分散を地道に計算するのは非常に面倒くさいです。
安心してください。分散と同様に計算を簡略化できます。
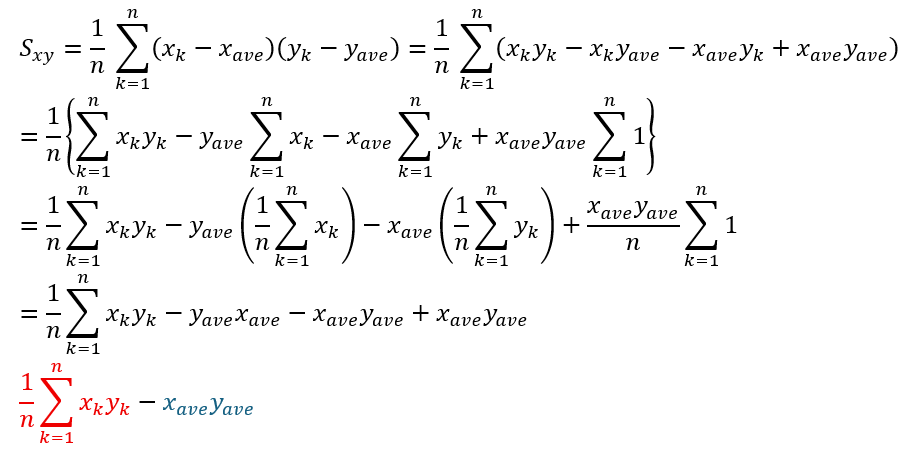
前回の記事でも解説しましたが平均値は絶対に変わらない値なのでΣの外に出せます。
- 赤い部分・・・積の平均値
- 青い部分・・・平均値の積
- 共分散は「積の平均値」から「平均値の積」を引いた量
相関係数の範囲
相関係数の範囲について解説します。
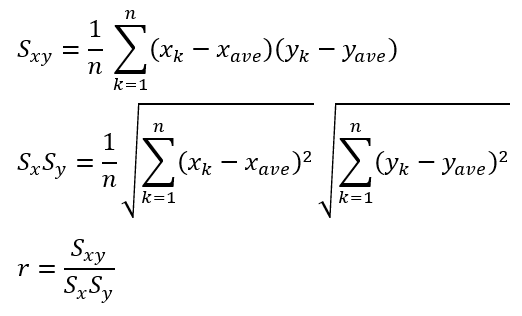
分母よりも分子は必ず小さいです。
また、相関係数の絶対値も1より小さいので「-1 ≦相関係数≦ 1」が成立します。
相関係数の比較
相関係数の比較に関して解説します。
相関係数で比較ができるのは「数字の大小による相関の序列」のみで、「相関の程度」は比較をすることはできません。
どういうことかというと、二つの散布図を考えたときに一方の相関係数が他方の2倍だったとしても、「相関の程度が2倍」ということは言えません。
言えるのは序列のみなので「一方の相関は他方と比較して正 or 負の相関が強い」ということのみが言えます。
相関関係と因果関係
相関関係と因果関係について具体例を用いて解説します。
以下の二つのデータについて考えてみます。
- 小学生100人の読書時間
- 小学生100人のテストの点数
- (ただし、二つのデータとも同じ100人のデータ)
この二つのデータを散布図にした時に強い正の相関関係があったとします(読書時間が多いほどテストで高得点を取った)。
このような場合、「読書時間が長いほど学力は高くなる」と断言しても良いのでしょうか?
一定数の人は「そのように断言してもいい」と答えるかもしれませんが間違いです。
何故なら、読書時間が長い(原因)ことで試験結果が良くなると言いきることはできないからです(他の要因もあるかもしれないし、全く関係ないかもしれない)。
相関関係があるからといって「原因と結果」の因果関係を断定することはできないです(科学では「データからそのような傾向がある」としか言えないです)。
特に、二つのデータが原因と結果に全く関係ないにもかかわらず散布図にした時に相関関係が生じていることを疑似相関といいます(相関関係の罠)。



コメント