こんにちは。Horyです。
前回の記事では電流の正体と連続体近似について学びました。
この記事で電流の正体は電荷の流れであり、時間変化する電荷を時間で微分したものであることも学びました。
今回の記事では電気抵抗とオームの法則について解説します。
皆さんは中学校でオームの法則をV=RIというように暗記していたと思いますが、なぜそうなるかをこの式で解説します。
今回も頑張りましょう。
抵抗の正体
まず、電流の正体は「電荷の流れ」であることは前回の記事でも説明しています。
電気抵抗は「電荷の流れを妨げる⇔電流が流れにくくなる」要素のことを言います。
ここで、以下に示すような導線中の電気量eを持った電荷一つを考えてみましょう。
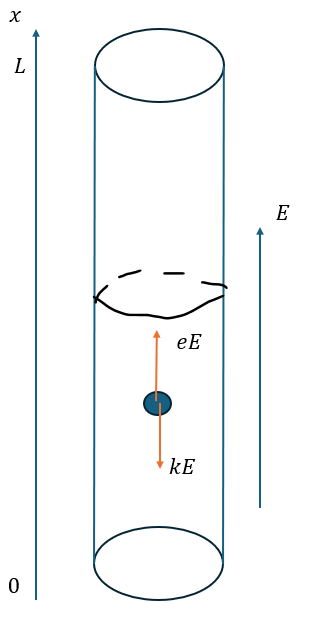
導線中の電荷は以下の二つの力を受けます。
- クーロン力eE・・・運動方向と逆向き
- 抵抗力kv・・・速度に比例する (運動方向と逆向き)
これを用いて運動方程式を立ててみます。
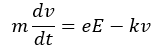
この形の運動方程式って見たことありますよね。
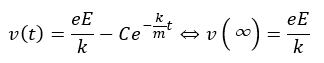
十分に時間がたつと電荷は等速運動しているとみなせます。
オームの法則の原理
ここで、何度も言っているようでしつこいと思いますが、「電流の正体は電荷の流れ」です。
上で示した導線の長さL, 断面積をSで一定とみなします。この導線内を電荷が単位体積当たりn個、速度v (一定とみなす)で運動しているとします。
時間がt経過後に断面を通過する電荷の量はQ=en(svt)と表せるので・・・
svtは時間tで通過する体積です。
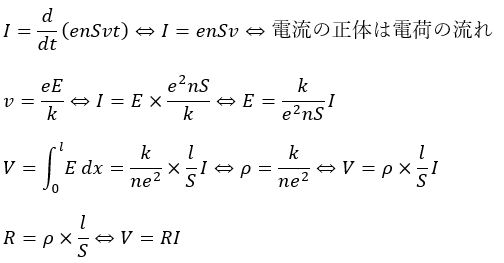
- I・・・電流;正体は電荷の流れ
- v・・・電荷の速度 (終端速度で一定)
- E・・・導線内の電場
- V・・・抵抗を持つ導線における電位差 (位置エネルギーの定義)
- ρ・・・電気抵抗率 (電流の流れにくさ)
- ρの逆数・・・電気伝導率(電流の流れやすさ)
- R・・・電気抵抗
- V=RI・・・オームの法則
電荷が抵抗力にされる仕事
抵抗がある導線内を電荷が上の図における位置x=0~Lまで動く間に電荷が抵抗力にされる仕事を求めます。
仕事の定義を用いて求めます。
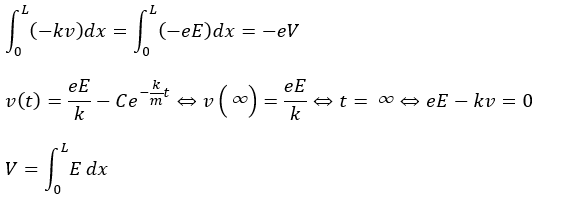
ただ、電荷は導線内に1個だけではありません。無数に存在します。
全ての電荷(N個あるとして)について、される仕事の和を求めてみましょう。
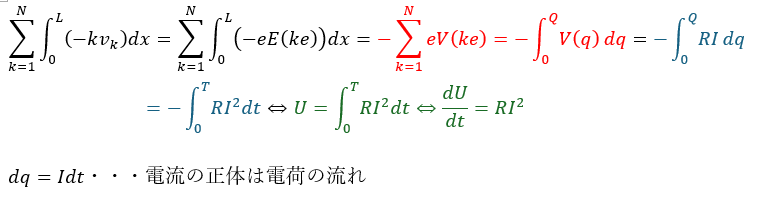
- 赤い部分・・・連続体近似 (前回の記事)
- 青い部分・・・電流の正体は電荷の流れ/オームの法則
- 緑の部分・・・抵抗で単位時間あたりに発生する熱;U



コメント