こんにちは。Horyです。
今回の記事では連結平面グラフにおけるオイラーの公式を解説します。
簡単に説明すると、立体の頂点・辺・面の数に関する定理のことで、この定理を正多面体に拡張すると「正多面体の個数は有限個」という結論を導き出すことが可能です。
今回はこの結論を導く前段階を分かりやすく解説したいと思います。
今回の記事は難しいかもですが頑張りましょう。
証明に関する事前知識
証明する前にいくつかの事前準備をしておかないといけません。
以下のことについて解説します。
- 平面グラフの定義
- 頂点・辺・面の定義
- グラフが連結であることの定義
これらについて個別に解説します。
平面グラフの定義
平面グラフの定義について解説します(これは、高校ではなく、大学のグラフ理論とかで触れられると思います)。
平面グラフとは「平面上の点(有限個)を結ぶことでできる線が交わらない図形」のことです。
これだけではピンとこないと思うので図に示します。
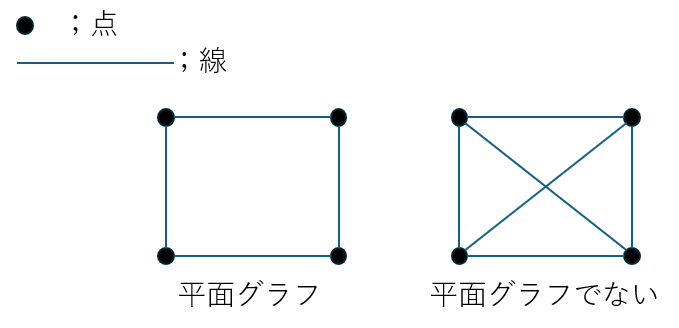
- 左の図形;平面グラフ (点だけが結びついていて線は交わってない)
- 右の図形;平面グラフでない (辺が交差している)
右の図形のように全ての点が結ばれている図形のことを完全グラフとも呼びます。
線が交差していなければいいので以下に示す図も平面グラフと言えます。
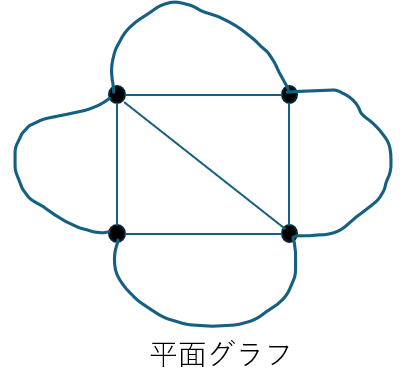
頂点・辺・面の定義
頂点・辺・面の定義を行います。
- 頂点・・・点
- 辺・・・点と点を結んだ線
- 面・・・辺によって囲まれて他の辺によって仕切られていない領域
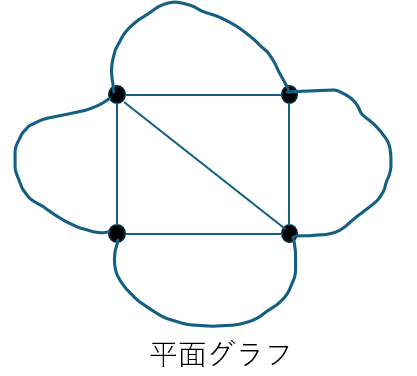
上の図形であれば・・・
- 頂点の数 = 点の数 = 4個
- 辺の数 = 線分の数 = 9個
- 面の数 = 辺で仕切られていない領域の数 = 6個
グラフが連結であることの定義
グラフが連結であるとは「平面グラフの点で任意にどの2点を選んでもそれらがいくつかの辺で結ばれていること」です。
言葉は非常に難しいですが言っていることは非常に簡単です。
連結グラフは以下の図に示すとおりです。
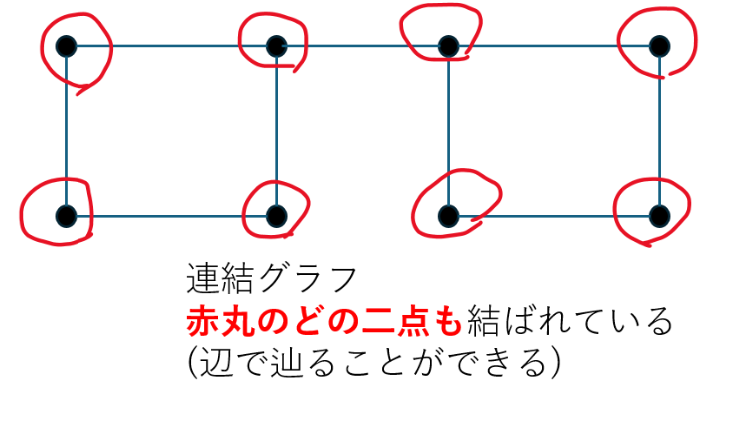
上のグラフで赤丸の点はどの二点をとっても辺で辿ることが可能です。
一方で以下に示すグラフは非連結といいます。

上のグラフの緑丸で囲った二点は辺で辿ることができません。
そのためこのグラフは非連結です。
オイラーの公式 証明
オイラーの公式とは頂点と辺、面の数に関して成立する以下の公式のことです。

オイラーの公式を数学的帰納法で証明します。
数学的帰納法に関する記事は以下に解説してあるので見ておいてください
証明のステップは以下の通りです。
- e=0のときに成立するのを示す (ステップ1)
- 辺の数が0のときの頂点と面の数は、、、?
- e≦kの時に成立することを仮定する
- e=k+1のときに成立することを示す (ステップ2)
これらについてステップごとに解説します。
ステップ1
これは考えるまでもないですが、辺の数が0個というのは平面上に一点しか存在しない場合しかありえません。
- e =0 ⇔辺の数が0個
- v =1⇔頂点の数は1個
- f =0⇔面の数は0個
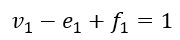
以上から辺の数が0個のときは成立します(当たり前)。
ステップ2
辺の数がk個以下の時に公式が成立するとします。
成立していると仮定した上で辺の数がk+1個あるときを考えます。
ただ、仮定したことを最大限利用したいので、辺の数を一つ減らすことを考えます。
(これにより公式が成立すると仮定したe=kの時を考えれる)
辺の数を減らすとできる図形には2パターンが存在します。
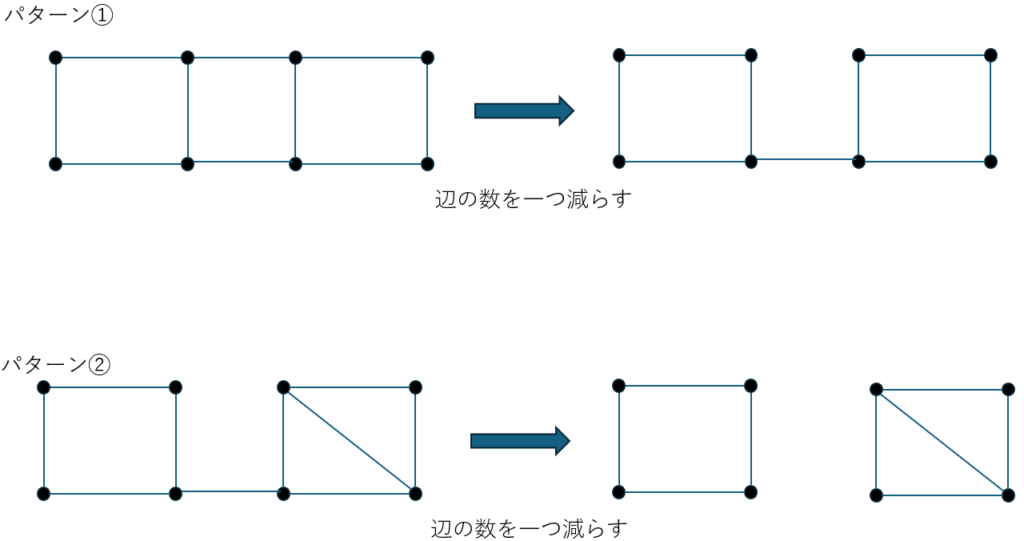
- パターン①;辺の数を減らして一つの連結グラフが完成する
- パターン②;辺の数を減らして二つの連結グラフに分かれる
パターン①とパターン②とで頂点や面の数がどうなっているかを考えます。
パターン①
頂点、辺、面の数を以下のように定義します。

辺の数を一つ減らしたところで頂点の数は変わりません。
しかし、面の数は一つだけ減ります。
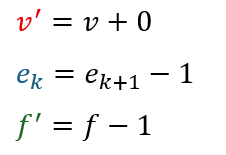
仮定した定義により以下の式が成立します。
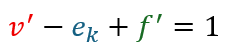
上の式に色がついた3つを代入すると・・・
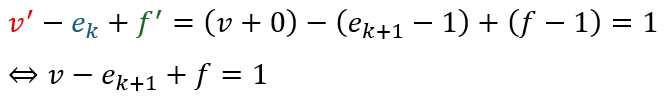
なので、辺の数がk+1個の時も成立します。
パターン②
パターン②は平面グラフが二つに分裂するので頂点・辺・面の数を以下のように設定します。

二つのグラフを合わせて考えると辺の数が一つ減ったところで頂点の数は変化しません。
また、当然ですが、面の数も変化しません。
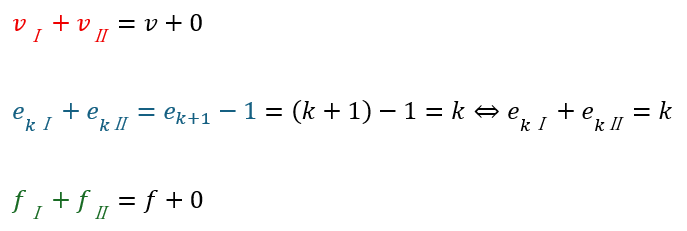
このことから、二つの分裂した部分の辺の数は必ずk個より小さくなります。
よって分裂した部分ごとに仮定した定理を流用できます。
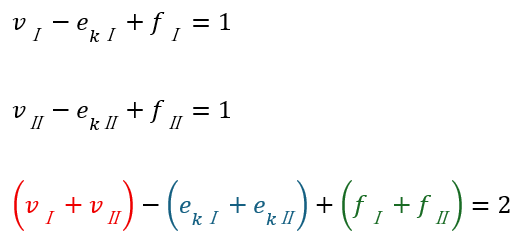
上の色がついた部分を代入します。
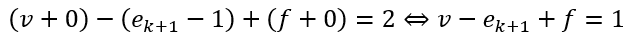
以上から辺の数がk+1この時でも成立します。
まとめ
以上の二パターンで辺の数がk+1個の時も求めたい式が成立すると証明できました。
数学的帰納法から連結グラフにおけるオイラーの公式が成立しました。
次回の記事でこの公式を正多面体に応用します。



コメント