こんにちは。Horyです。
この記事でもいよいよ積分について話すことになりました。積分には二つの意味がありますが、今回の記事で話すのは計算としての積分の意味です。
今回も頑張りましょう。
積分をやる前に微分の計算は完璧ですか?というのも、そもそもですが、微分の計算が完璧にできないと積分はできません。そのため、この記事を読む前に微分が完璧でなければ微分の記事を読んでおいてください。
原始関数
最初に原始関数についてです。
原始関数と聞くと学生は頭を抱えますが、何ら難しい話ではありません。

たったこれだけのことです。なので、原始関数と聞いても恐れないでください。
不定積分について
不定積分について話します。f(x)の原始関数の一つをF(x)と置きます。先ほど「原始関数の一つ」という表現を使いましたが、理由は以下に説明します。
ところで、積分の記号を簡単に説明します。
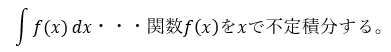
この積分記号の意味を言葉で説明できるようになってください。続いて、任意の関数f(x)とその原始関数の関係について積分記号を用いて表します。

先ほど、「原始関数の1つ」と言った理由ですが、積分定数Cの値を任意に変えれるからです。また、不定積分の基本公式を以下に示します。
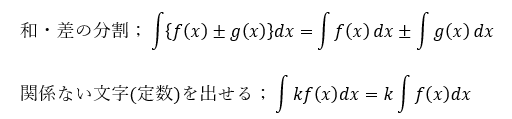
「積分計算は微分の逆演算」というのは正しく思えますが、間違いです。理由は実際にやってみると分かります。関数f(x)の原始関数を考えると・・・
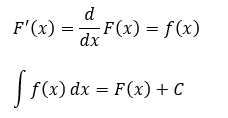
上の式を見ると逆演算になっていません。積分定数を無視できないからです。ただ、積分と微分が表裏一体の関係というのは間違いないです。
不定積分の計算で積分定数は絶対に忘れないでください。
微分法と積分計算
微分法で導出した導関数を応用すれば様々な関数の積分は以下のようにできます。
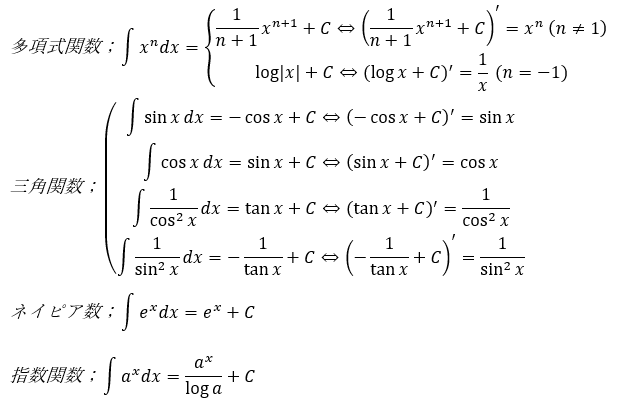
定積分について・・・
定積分とは、積分変数に範囲がある積分のことです。そのため、積分定数は出ません。
原始関数を利用して定積分の計算を示します。
計算の意味を言葉で説明できるようになってください。

定積分の公式
以下にまとめるのは定積分の重要公式です。一部証明しないモノもあります。
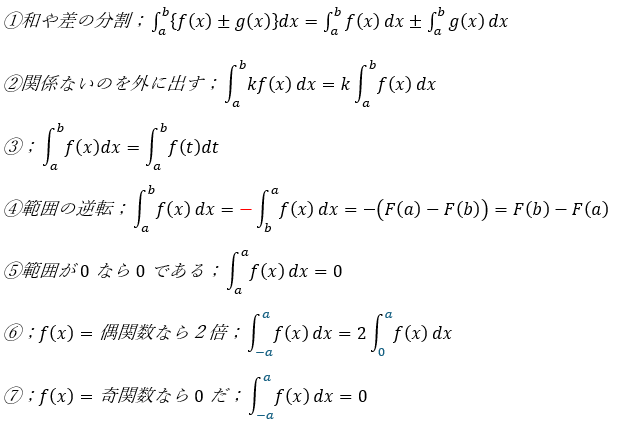
特に、④の公式は重要です。また、⑥と⑦については、積分する範囲に対称性がないとダメです(-aから+aのように・・・)。



コメント