こんにちは。Horyです。
前回の記事で直交座標と極座標についての運動方程式変換について話したのちに、円運動について説明しました。
まだ記事をご覧になっていない方はこちらの記事をご覧ください。
今回の記事では等速円運動と非等速円運動について解説し、これに関連して単振動の応用である単振り子についても解説します。
また、私は円運動の運動方程式は必ず静止極座標で記述します。
今回も頑張りましょう。
等速円運動
以下に示すのは等速円運動に関する問題です。

この問題を例に解説します。以下に図を示します。
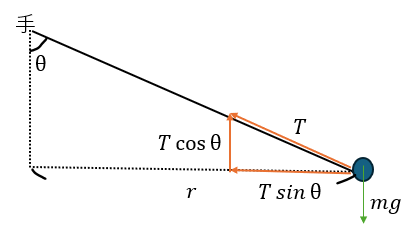
等速円運動 解答・解説
問題の解答・解説です。以下の3つの運動方程式を書きます。
- 円運動の動径方向・・・拘束条件を思い出す
- 円運動の接線方向・・・等速で速度が一定
- 水平面について垂直な方向・・・小球の高さは変化しない
また、等速であることから角速度も一定です。
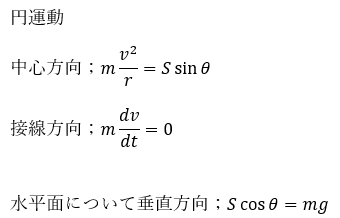
この3つの式を用いれば導出できます。
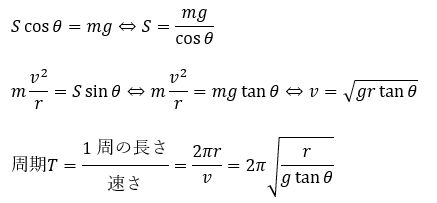
非等速円運動
以下に示す問題は非等速円運動についての問題です。

この問題を例に解説します。状況を図に示します。
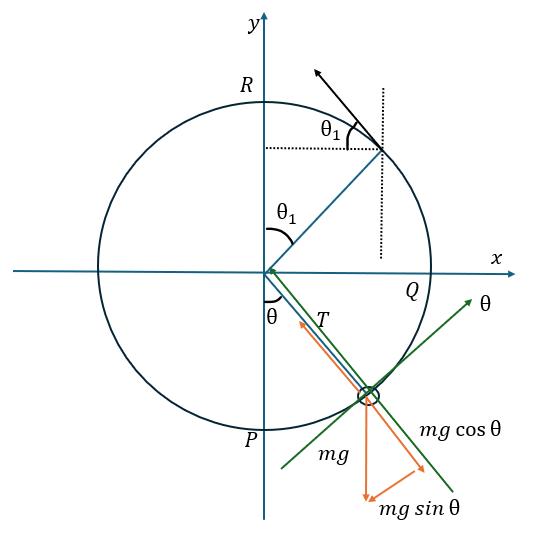
ここで、速度に関する条件をまとめます。
- v1≧vR⇔小球は点Rを超えて円運動
- v1≧vQ⇔小球は振り子運動
- vQ<v1<vR⇔θ=π-θ1で糸がたるむ
また、先ほどの問題では速度が一定(角速度も一定)でしたが、本問では速度が一定ではない(角速度が一定でない)ことに注意してください。
(1)解答・解説
まずは、円運動の中心方向と接線方向の運動方程式を立てて、角速度についての式を記述します。
この問題はエネルギー保存則とかも使います。
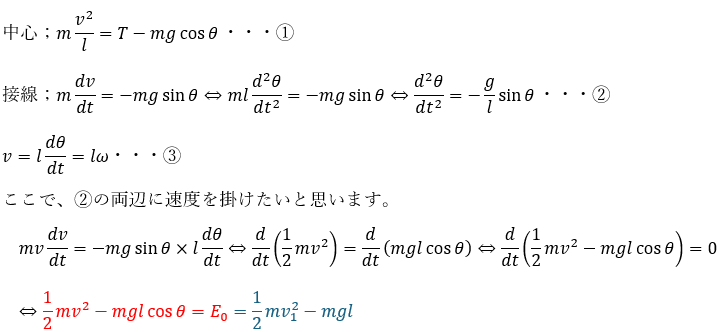
上の式がエネルギー保存則です。図を用いてよく考えてみれば当たり前のことです。
ただし、位置エネルギーの基準(位置エネルギーが0である点)を点Oにしている事には注意が必要です。
- 赤い部分・・・エネルギー保存則
- 青い部分・・・最下点での小球のエネルギー
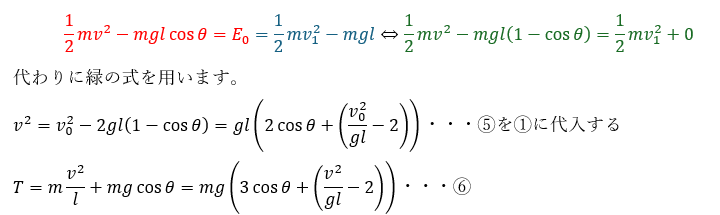
(2)~(4)解答・解説
先ほどの⑥の式にそれぞれのθを代入し、その時に、糸がたるむ、つまり張力が0になる速度の条件を求めれば良いです。
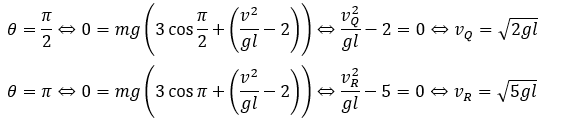
(4)については自習とします。ここまでできたならできると思うので頑張ってください。
単振り子について・・・
単振動の応用に単振り子というモノがあります。
以下に問題を示します。

この問題を例に解説します。Δθがめちゃくちゃ小さく0に近似できるのがポイントです。
解答・解説
中心方向と接線方向の運動方程式を記述します。
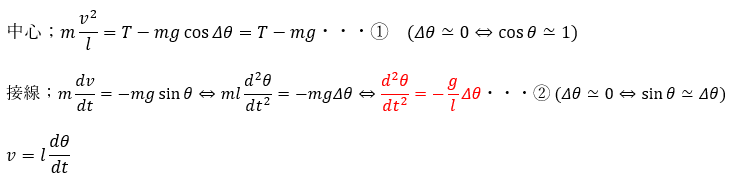
上の式の赤い部分が単振動(単振り子)の式になります。
つまり、θがどうなるかを記述することで物体の位置を記述できるわけです(運動が円周に拘束されていればθが分かった時点で物体の位置は極座標で記述可能)。
ここからは単振動の運動方程式(微分方程式)に帰着できます。




コメント