こんにちは。horyです。
今回の記事では等差数列と等比数列が入り交じった数列の和の公式の導出法を原理から説明しようと考えています。
等差数列と等比数列に関する記事はこちらです。
まだ読んでいない人は本記事を読む前に読むことをお勧めします。
それでは、今回も頑張りましょう。
等差数列と等比数列の入り交じった数列
まず、等差数列と等比数列の入り交じった数列は以下のような数列のことです。
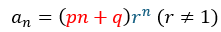
上の数列で赤い部分が等差数列・青い部分が等比数列です。この数列の和を求めてみましょう。
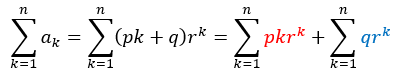
問題は赤い部分をどうやって処理するかですが、公比を掛け算したものを引き算することで突破口が開けます(定石なので手順は覚えてください)。
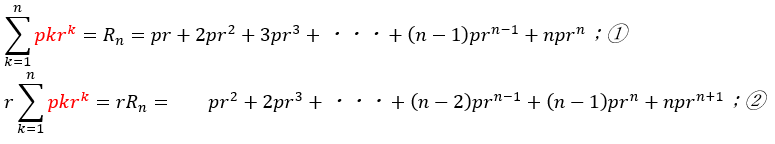
①から②を上下に引き算します。
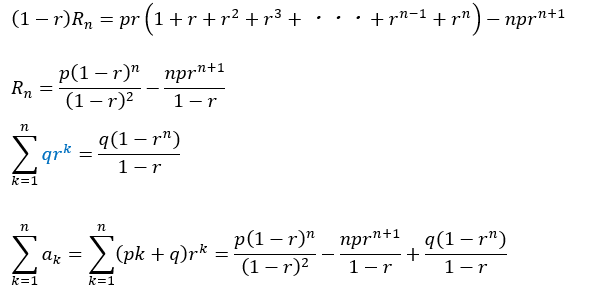
以上により、初項から第n項までの和を求めることに成功しました。
問題
以下はこの記事で取り組む問題です。

この問題を例に解説します。
(1)は普通の等比数列の和です。一方で、(2)・(3)は等比数列と等差数列が入り交じった数列の和です。
(1)~(3)ですが、意外な落とし穴があるので注意してください。
(1)解答・解説
(1)の解答・解説です。
この数列は初項が1で公比がxの等比数列と見ることができます。
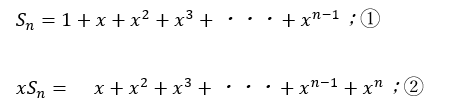
①から②を上下方向に引き算します。
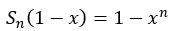
ここで、このブログで何回も言っていることですが、0で割ることはできません。そのため、場合分けが必要です。等比数列の和を求めるとき、公比が文字の時は必ず意識してください。
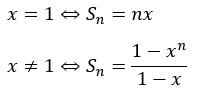
(2)解答・解説
(2)の解答・解説です。
等差数列と等比数列が入り交じった数列です。

上の式の赤い部分は(1)で求めました。当然、場合分けもあります。
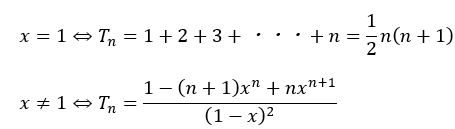
(3)解答・解説
(3)の解答・解説です。やり方は(2)と同じようにやります。
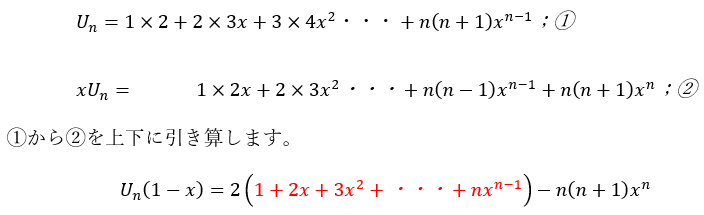
上の式の赤い部分は(2)の答えです。当然、場合分けもあります。
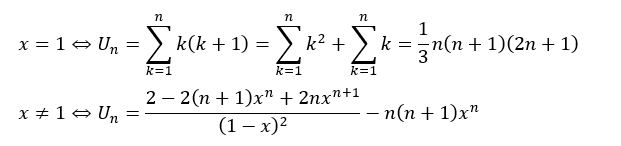



コメント