こんにちは。Horyです。
だいぶ前に書いた記事なのですが、場合の数と最短経路に関して解説したと思います。
今回の記事は上の問題の応用問題です。
上の記事では平面な道における最短経路でしたが、もしも、これが立体図形になったらどうなるでしょうか?
解ける人はかなり少ないように思いますので解説します。
今回も頑張りましょう(今回は上の記事を読んでいることが前提となりますので、まだの人は読んどいてください)。
立方体と最短経路
以下はこの記事で取り組む問題です。

この問題を例に解説します。
まずは、特定の点を決めて各頂点を記号で表します。
今回なら特定の点をGとして、アルファベットで決めていきます。
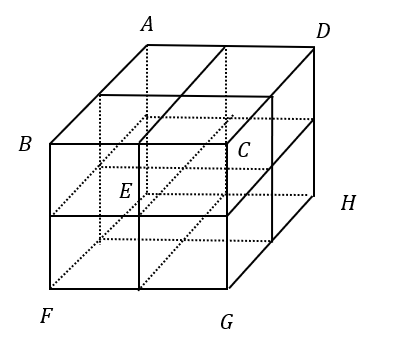
いきなり最短経路を求められるわけないと思いますが、必ず誘導が付きます。安心してください。
手順は以下の通りです。
- G → C → Aの数
- G → 辺BCの1点 → Aの数
- G → 辺BC or CDの一点 → Aの数
- G → 辺EF or EHの一点 → Aの数
この手順に沿って求めていきます。
前回の記事でも紹介したポイントですが、立体のまま考えると厄介な場合があるので展開図で考えます。
G→ C→ Aの数
展開するまでもないので立体図形のまま考えます。
- G→C;1通り
- C→A;2×2の正方形
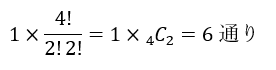
G→ 辺BCの1点→ Aの数
長方形GDAFで展開図を考えると、平面に帰着できます。
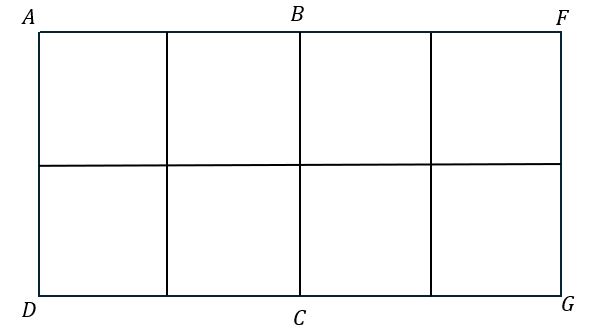
これはどんな道筋を辿ったとしても必ずBとCは通るので・・・
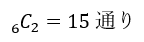
G → 辺BC or CDの1点 → Aの数
- 辺BCの1点→展開図GDAFで求めた15通り
- 辺CDの1点→展開図GBAHで求める 15通り
- C→ Aは6通りが重複している
何で6通りが重複しているかというと以下の図を見ていただきたいです。
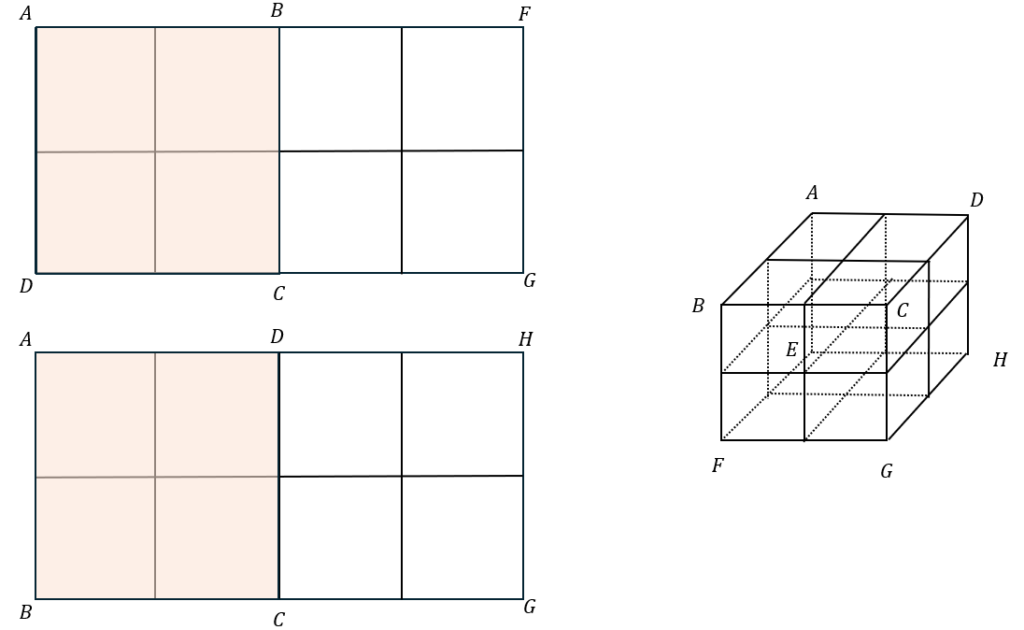
どちらの展開図もオレンジ色の部分は同じ面になります。だからG→C→Aまでの6通りは重複しているのです(ダブルカウント)。
よって場合の数は、15+15-6 =24通りです。
G → 辺EF or EHの一点 → Aの数も同様に24通りです。
G→Aまでの総数
問題はA→Gまでの総数を求めることです。
もう傾向はつかめたと思いますが、ベン図を作ってみます。
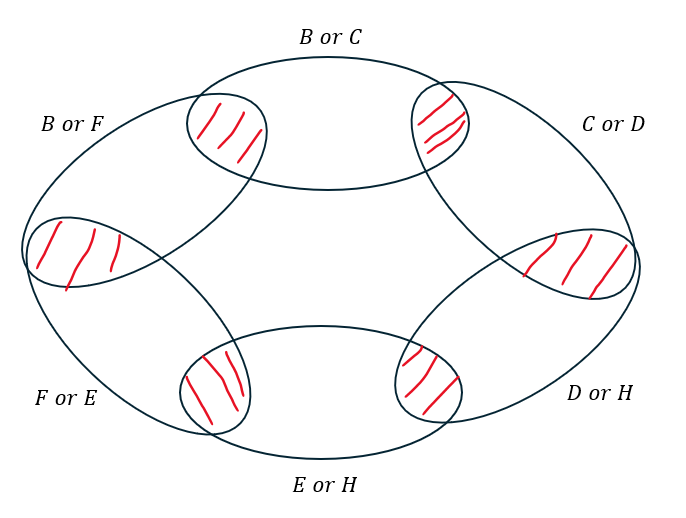
上の丸の部分1つにつき15通りです。
一方で斜線部の赤の部分は全て6通りです。
よって、丸を全部足して赤の部分をダブルカウント分だけ引けば良いので・・・
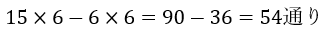



コメント