こんにちは。Horyです。
確率の記事で最大値に関することは触れていませんでした。
今回の記事では確率で最大値を求める方法について原理から解説します。
今回も頑張りましょう。
確率の最大値
以下に示すのはこの記事で取り組む確率の最大値に関する問題です。

この問題を例に解説します。
(1)解答・解説
- k回目までは全て異なる⇔ n個の異なる数から k個を「選び並べる」
- k+1回目に既出の k種類と同じボールを取る
- 分母;n個の選択肢が k+1回
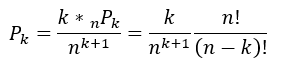
以上が答えになります。
これを利用するのが次の問題になります。
余談ですが、順列のPや組み合わせのCをPやCを用いずに表す方法は知っておいた方がいいと思います。
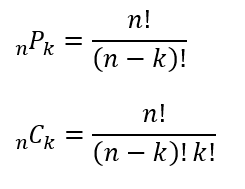
(2)解答・解説
確率で最大値を求める問題が出てきたら、Pkに対して1つ数が多いPk+1を考えてほしいです。
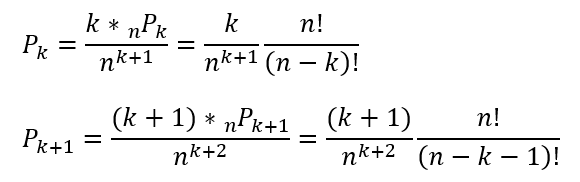
そしてPkとPk+1の比を考えて1との大小を考えればいいです(比が1になるときのkを求める)。
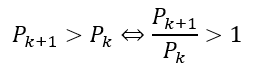
どういうことかというと、確率が増加して減少する場合、前後の確率の比は・・・
- 増加しているとき・・・確率の比は1より大 (Pk+1>Pk)
- 減少しているとき・・・確率の比は1より小 (Pk+1<Pk)
- 最大のとき・・・比が1に最も近づく
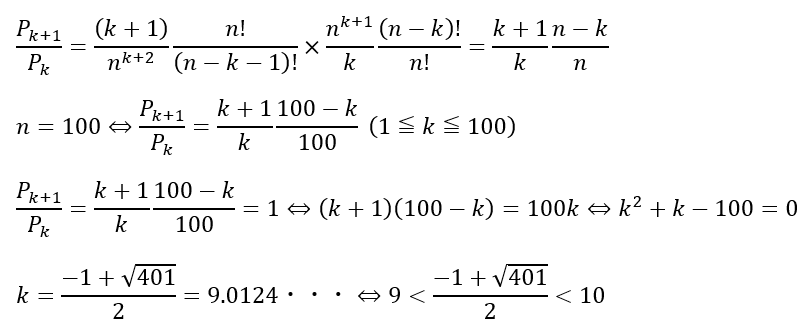
以上から以下の不等式が成立します。
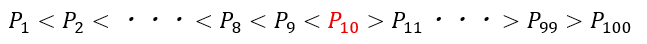
実際にやってみると・・・

よって最大値は(10+1)回目に試行が終了する確率です。
(2)別解;微分を用いる
別解として数Ⅲの微分を用いる方法もあります。
ただ、面倒くさいので特別な事情がない限りやらない方が良いかもです。
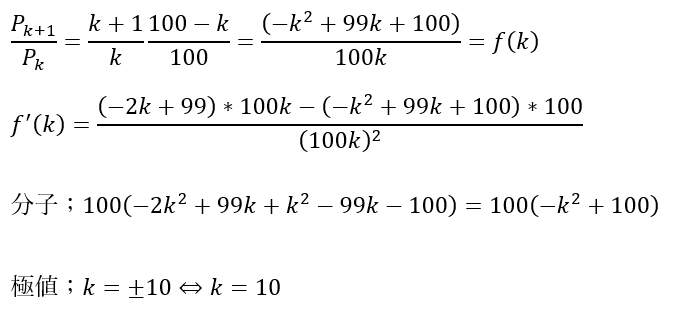
後は増減表を書いてグラフの推移を追っていけばk=10の時が最大値を取ることが分かります。



コメント