こんにちは。Horyです。
今回は確率の問題について、問題が同じであっても文章が違うことで答えが違ってくるような面白い問題を紹介します。
今回も頑張りましょう。
「決めておく」と「選ぶ」の違い
以下に示すのはこの記事で取り組む問題です。

この問題を例に解説します。頑張りましょう。
問題に関して、A,B,Cの3人がいて人が降りるのは2~5合目(4合分)のどれかです。
ということは、どの合でも二人以上が降りない(一人だけ降りる)としても、1つだけ人が降りない合がでてくることになります。
どの合で人が降りないかで場合分けするのが効果的です。
- 二人以上降りない⇔3つの合で一人ずつ降りる
注意として、5合目まで残っていた人は5合目で必ず降りるとします。
(1)解答・解説
各人がどの合で降りるかを勝手に決めておく場合です。
文章的に「勝手に」というのは「あらかじめ」や「事前に」と置き換えても良いです。
つまり、事前に2~5合目のどこで降りるかを決めておくのです。

仮に2合目で人が降りないとして、3,4,5合目で一人ずつ人が降りる確率を求めていきます。

これは、人が降りない合が3~5合目でも同じなので求める確率は・・・
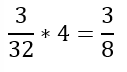
(2)解答・解説
2,3,4合目で各人が降りるか降りないかを選ぶ場合を考えます。
これは、合に到着した時に「降りる」or「降りない」の2択の選択肢が表れて各人が選択肢に従って決めるという場合になります。
ただし、5合目まで残った人は5合目では必ず降ります。
どちらの選択をするかはもちろん「1/2」です。

- 赤文字;2合目で誰も降りない
- 青文字;3合目で3人のうち1人が降りる (3C1・・・誰が降りるの?)
- 緑文字;4合目で2人のうち1人が降りる (2C1・・・誰が降りるの?)
- 黒字;5合目まで残った人はそこで降りるしかない。だから1

- 赤文字;2合目で3人のうち1人降りる
- 青文字;3合目で2人とも降りない
- 緑文字;4合目で2人のうち1人が降りる
- 黒字;5合目まで残った人はそこで降りるしかない。
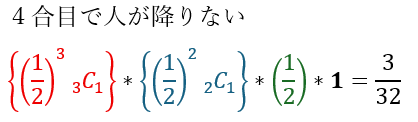
- 赤文字;2合目で3人のうち1人降りる
- 青文字;3合目で2人のうち1人降りる
- 緑文字;4合目で降りない
- 黒字;5合目まで残った人はそこで降りるしかない。

- 赤文字;2合目で3人のうち1人降りる
- 青文字;3合目で2人のうち1人降りる
- 緑文字;4合目で1人降りる
よって求める確率はこれらの足し算になるので・・・
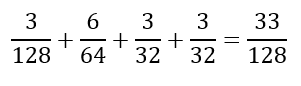



コメント