こんにちは。Horyです。
皆さんは、確率の有名な問題でモンティホール問題というのを知っていますでしょうか?
確率の世界では有名な話なので知っている方も多いと思いますが、この問題は数学者も間違えたと言われています。
今回はこの問題に関して解説を行うと共に確率の小話を話したいと思います。
今回も頑張りましょう。
モンティホール問題
モンティホール問題の概要を以下に示します。

上に示すのがモンティホール問題です。
言葉だけでは非常に分かりにくいので図を示します。
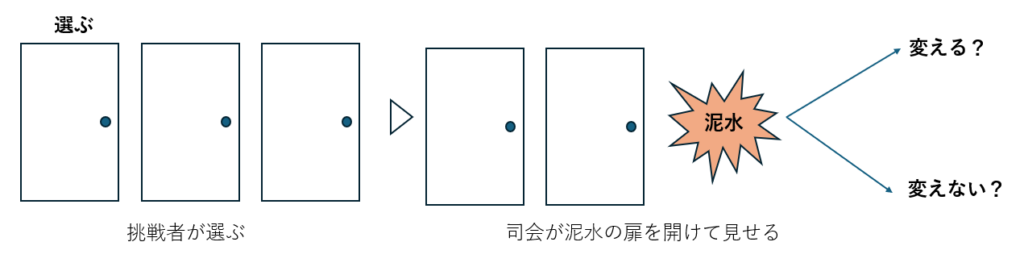
結論から言うと「変える」方が泥水に入らなくて済む確率が上がります。
何でかを考えてみましょう。
極端な場合を考える
モンティホール問題で最初は「変えない」という結論を導き出した人の方が多かったです。
「変えない」というのは結果的に誤りです。
間違えた原因は「扉の少なさ」にあるのではないかと私は考えています。
確率では極端な場合を考えて実験するのが効果的です。
仮に扉の数が100個だったとしたらどうでしょうか?
- 挑戦者は100個の扉から1つ選ぶ
- 司会者は残りの扉の内、泥水がある98個の扉を開けて見せる
- 変える or 変えない
図を用いて考えてみます。
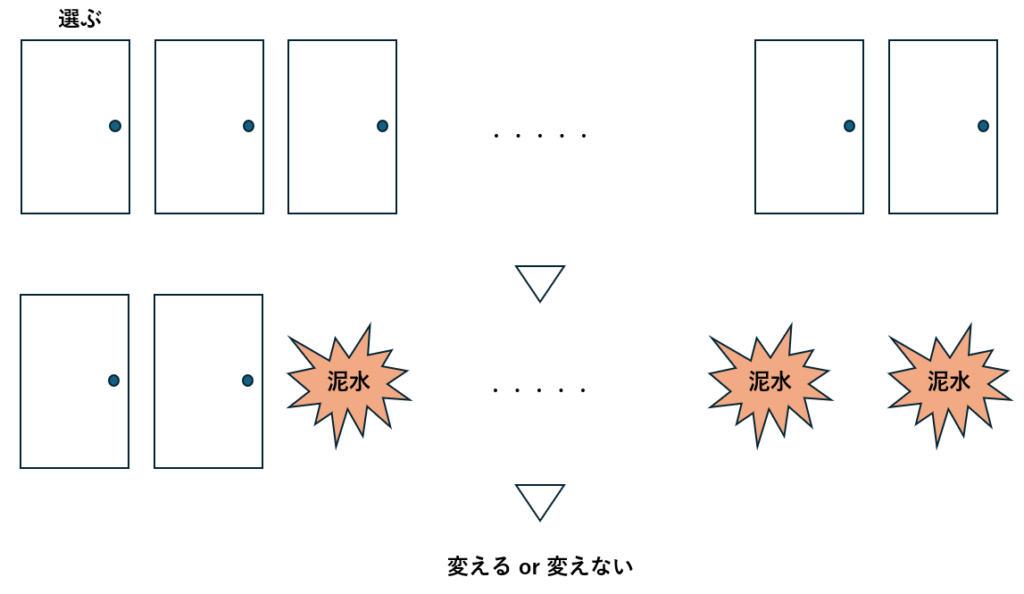
常識的に考えて変えた方が良いと分かると思います。
ただ、これだと論理的な説明になっていないので深掘りした解説を行います。
解答・解説
ここでは、簡単のために扉にA,B,Cという名前をつけたいと思います。
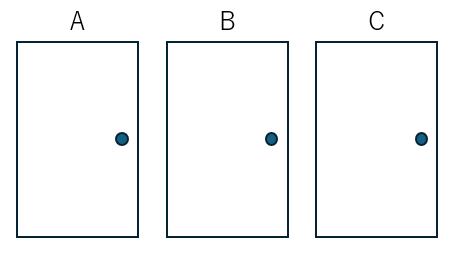
ここで、挑戦者はドアAを選ぶと仮定します。
分かりやすいように表を用いて考えます。
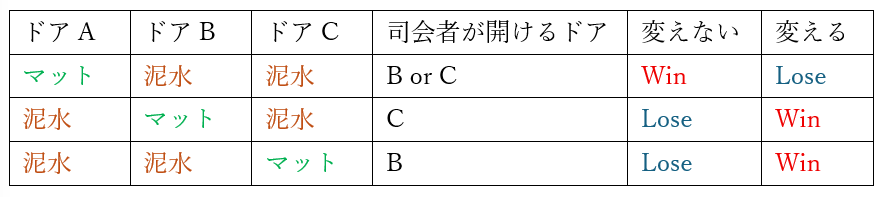
上のように考えると変える方がWinの数が多いので確率的に泥を浴びない可能性が高くなります。
これは挑戦者がB or Cのドアを選んでも同様の議論になるので変えた方が良いです。
場合の数・確率が難しい理由
モンティホール問題を数学者が間違えてしまったように、確率や場合の数が難しいと感じることは良くあります。
また、面白い事に、模試などで確率や場合の数の問題を出して文系と理系で平均点を出すと文系の方が高くなる傾向があります(あくまで個人の見解だが・・・)。
場合の数や確率で用いるのは以下の記事でも書いたように中学校で習う「和の法則」・「積の法則」です。
順列や組合わせのCやPがあるかもしれませんが、それらも元を辿れば「和の法則」・「積の法則」に帰着できます。
なのに、どうして「場合の数」や「確率」が難しく感じて、文系の方が平均点が高くなるのか・・・
それは、この分野の問題が単なる数学の問題でなく、国語などに見られる読解力の問題でもあるからです。
- 問題のテーマ
- くじ引き型・玉取り出し型
- トランプ(カード)
- じゃんけん
- コイン
- サイコロ
- 最短距離
- 図形
- 方程式
- 組み分け (区別ある or ない)
- 方法
- 同時に取り出す
- 1つずつとる
- 取った後に戻す
- 取った後に戻さない
- 取った後に追加する
- 取ったモノを交換する
このように「多数のテーマ」と「多数の方法」が掛け算で組み合わさり問題のパターンが莫大になってしまうことが学生を苦しめている理由です。
これを攻略するには「慣れ」しかありません。
慣れることで問題を見た瞬間にどの「どういう考え方で」「何を使うか」思いつくレベルになるとgoodです。



コメント