こんにちは。horyです。
今回は特殊不等式の1つである相加・相乗平均について簡単にまとめると共に、間違いやすいポイントを解説しようと考えています。
相加・相乗平均とは
以下に最も簡単な相加・相乗平均についてまとめようと思います。
「x, y」は正の実数とするとき、以下の不等式が成立します。

一応、証明してみます(左辺から右辺の引き算を実行)。
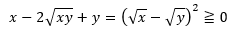
また、不等式で等号が成立することを等号成立条件といいます。
上の式での等号成立条件は以下のようになります。
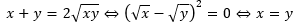
相加・相乗平均の注意点を簡単にまとめます。
- 各項が0以上の実数である必要がある
- 等号成立条件=最小値とは限らない(後で説明)
また、以下の式の形を見たら結構使えます。このタイプの関数は等号成立条件で必ず最小値を取ります。「x」は正の実数とする。
問題 相加・相乗平均 自然数nへの拡張
先ほどは二文字の相加・相乗平均について考えましたが、これをn個の文字に拡張します。
以下は問題です。

この問題を簡単に説明します。
相加・相乗平均の一般化です。別にできなくても構わないですが、頭に入れておいた方が良いです。
(1)解答・解説
(1)の解答・解説です。
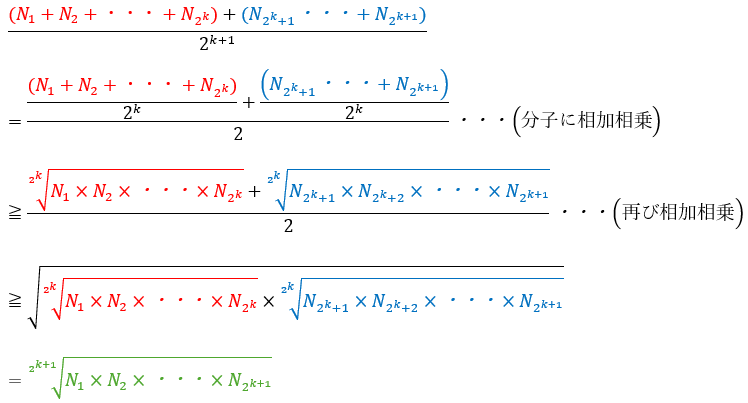
以上により成立することが分かりました。
(2)解答・解説
(2)の解答・解説です。
以下のk+1個の項をn=k+1の時の定理に応用します。
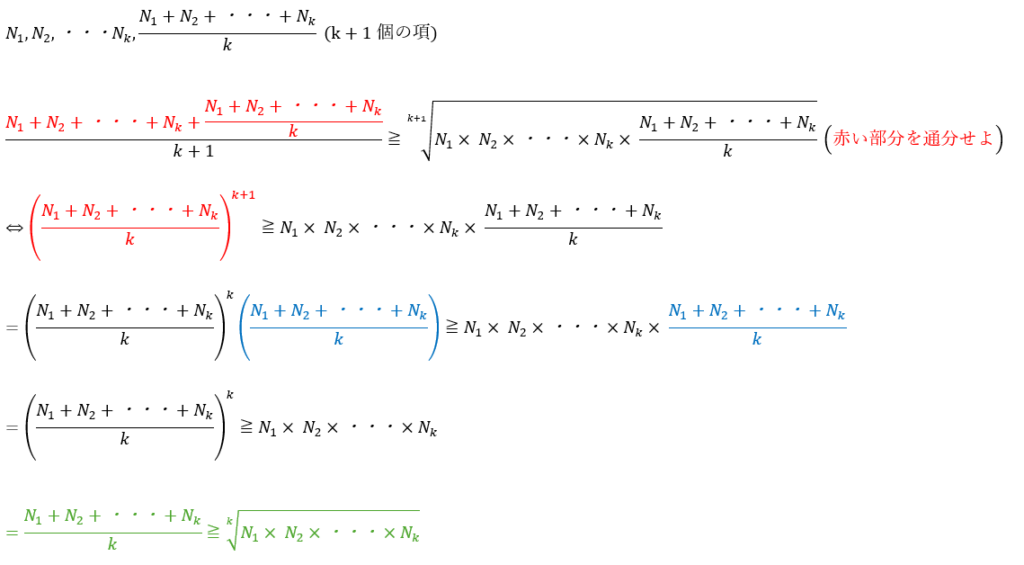
以上により成立しました。
結局なにが言えるのか・・・
先の証明問題で結局何が言えるのかですが・・・

相加・相乗平均の間違いやすい問題
以下は関数の最小値を求める問題です。
相加・相乗平均を用いても良いですが、間違いが起こりやすいです。
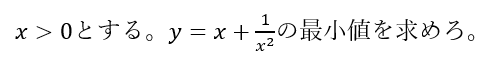
この問題を例に解説します。
間違った解答
まず、間違った解答を紹介します。
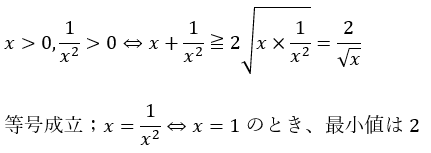
この解答は間違いです。
以下に間違いである理由を簡単に説明します。関数を以下のように定義します。
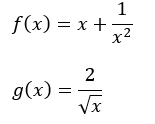
上の答案はあくまで、y=f(x)のグラフがy=g(x)のグラフの上側にあって、「x=1」となる点で共有点を持つことを示しただけに過ぎません。
x>0を満たす点でf(x)≧2が成立するかは分かりません。
実際にxが次の値の時を考えると・・・
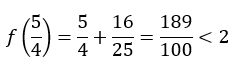
2より小さい値になるので最小値は2ではありません。
だから、「等号成立条件時のx=最小値」と考えるのは危険です。
正しい解答
相加・相乗平均を用いた正しい解答は・・・
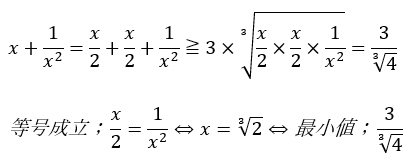
以上が正しい解答です。
ただ、この問題で相加・相乗平均を簡単に思いつくことは難しいので、数Ⅲの微分を知っているのであれば微分で増減表・グラフを書いて示した方が早いと思います。



コメント