こんにちは。Horyです。
今回の記事は直線や平面、空間を分割したときにできる有限区間と無限区間の数を求める問題を解説します。
今回も面白い問題なので頑張りましょう。
直線線の分割
以下の問題は直線の分割に関する問題になります。

この問題を例に解説します。
図もなしに考えるのは難しそうなので簡単な状態で実験してみましょう。

上の図はn=3で3個の点が置かれています。
- 有限区間の数・・・2個
- 無限区間の数・・・2個

上の図はn=4で4個の点が置かれています。
- 有限区間の数・・・3個
- 無限区間の数・・・2個
傾向がつかめてきたので解答に移ります。
解答・解説
直線にn個の点を置くと右端と左端を仕切ることはできません。
無限区間;2個 (半直線の数は常に2本)

以上から・・・
- 無限区間;2個
- 有限区間;n-1個
平面の分割
平面の分割に関する問題です。
ここから難易度が跳ね上がります。

この問題を例に解説します。
「直線が平行にならない」∧「直線の一致がない」というのは座標平面で三角形が完成する条件です。
この問題の突破口ですが、1つの直線が他の直線と何個の交点を持つかを考えるところから始めます。
交点が一つの直線をいくつに分割するかを考えることで、前の問題を利用できます。
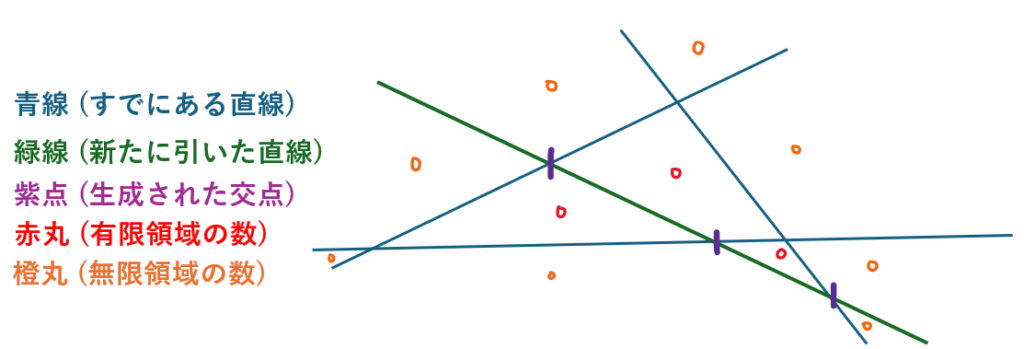
解答・解説
- n+1本目の直線について
- n+1本目の直線とすでにあるn本の直線との交点;n個
- n+1本目の直線
- n個の交点を新たに生成 ⇒n-1本の線分を生成 ⇒n-1個の有限領域を生成
- 2本の半直線を生成 ⇒2個の無限領域を生成
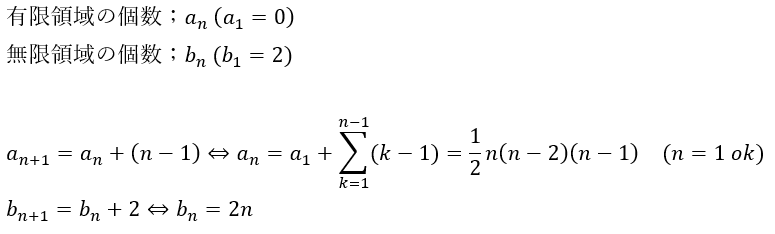
有限領域の個数については階差数列が応用できますね。
空間の分割
空間の分割に関する問題です。

この問題を例に解説します。
「全ての平面が平行でない」∧「同一平面上にない」というのは座標空間で四面体が完成する条件です。
この問題の突破口ですが、1つの平面が他の平面と何個の交線を持つかを考えるところから始めます。
解答・解説
- n+1枚目の平面について
- すでにあるn個の平面とn本の交線を新たに生成
- n本の交線について
- 有限領域・・・an個を生成
- 無限領域・・・bn個を生成
- 新たな有限空間の生成数 = 新たな有限領域の生成数
- 新たな無限空間の生成数 = 新たな無限領域の生成数
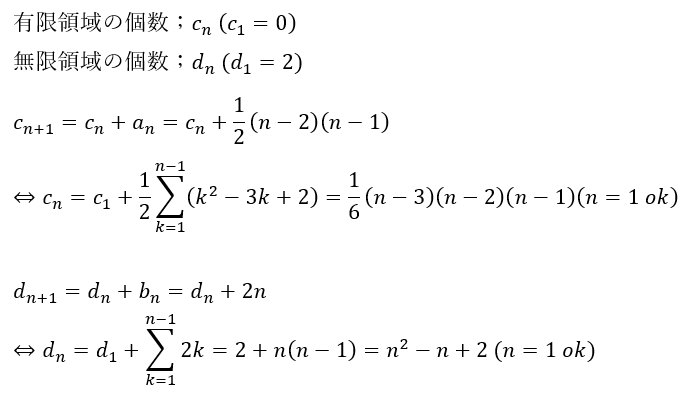
以上が解答になります。
空間に関しては問題が非常に抽象的なので図に描くことも難しすぎます。
この問題ができたら大したもんです。



コメント