こんにちは。Horyです。
これまでに私たちは数学ⅠAⅡBの様々な立体問題を解いてきました。
今回の記事では球に内接する直方体の問題を解いていきます。
本問は上の記事に示すような問題とは少し違って数Ⅱの知識を用います。
今回も頑張りましょう。
球に内接する直方体
以下に示すのは球に内接する直方体に関する問題です。

この問題を例に解説します。
問題を解く前の下準備
まずは、問題を解く前の下準備です。
図を描いてみましょう。
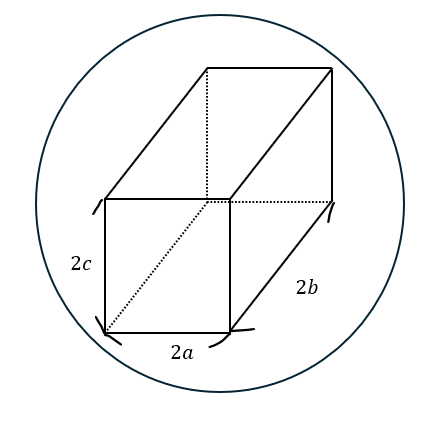
図形量の最大・最小では変数を決めるところから始めます。
今回は辺の方がやりやすいので変数を辺とします。
また、自分の都合の良いように座標を設定します。
今回は球の中心を原点とします。
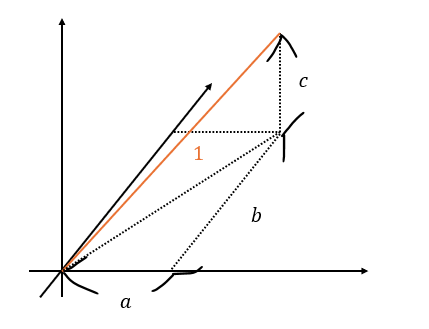
上の図のオレンジの線の長さは1と分かります(球に直方体が内接しているので、直方体の全ての頂点は球面に存在する)。
これらを起点に問題を解いていきましょう。
表面積Sを辺の長さで
表面積Sを辺の長さで表してみます。

ここで、対称式の性質を利用します。
①を変形させてSや lの式を出すことが出来れば目的達成です。
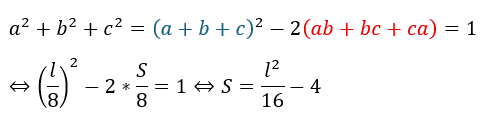
表面積の最大値
表面積を全辺の長さで表すことが出来ました。
- Sが最大のとき ⇔ lも最大である
- 条件①という制約の下でlの最大を求める
方針を立てることが出来ました。
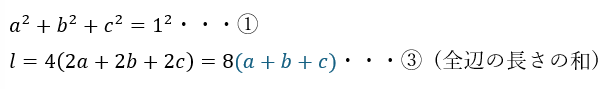
この2つの式ってどこかで見たことがありますね。
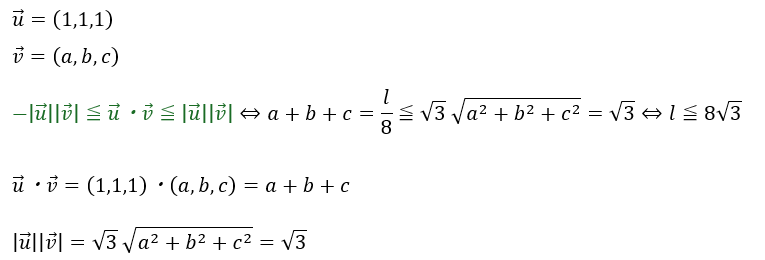
上の緑の不等式はコーシー・シュワルツの不等式です。
この不等式については上の記事にも書いてあります。
本不等式はデータの分析でも出てきますので興味あったら以下の記事も読んどいてください。
- 不等式の最右辺・・・2つのベクトルのなす角が0°
- 不等式の最左辺・・・2つのベクトルのなす角が180°
- ベクトルu・・・式①の長さの2乗に関する係数のデータ
- ベクトルv・・・直方体の辺の長さに関するデータ
- ベクトルのなす角θ・・・cosθは2変量の相関係数という見方が出来る
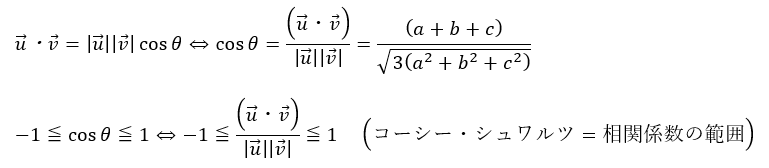
以上から表面積Sの最大値は・・・
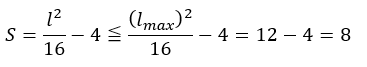
以上から表面積の最大値は8です。



コメント