こんにちは。Horyです。
前回の記事では熱力学の定積・定圧・等温過程に関する解説とこれらの状態に遷移する問題の攻略を行いました。
上の記事で解説していない熱力学の変化が断熱過程です。
断熱過程には種類があって・・・
- 準静的断熱過程
- 断熱自由膨脹過程
上の二つの種類に分けることができて問題の解き方や考え方が変わってきます。
今回紹介するポアソンの公式は準静的断熱過程に関する公式になります。
今回も頑張りましょう。
ポアソンの公式の導出
断熱過程とは熱の流出や流入を0にした変化過程のことです。
そして、ポアソンの公式は準静的断熱過程での公式になります(断熱自由膨脹とは全く別)。
京都大学はポアソンの公式がかなり好きで誘導付きの導出問題を出すときがあるので覚えておいた方がいいです。
準静的過程に関してはこちらの記事に示すとおりです。
まぁ、問題で学んだ方が早いと思うので問題を以下に示します。

上の問題を例にポアソンの公式を導出します。ちなみに、(2)で導出する式がポアソンの公式と呼ばれているものです。
余談ですが、PとVの比が一定とありますが、実際は一定ではありません(ポアソンの公式を見ても明らか)。ただ、Δを微小量であるとして、直線的に近似できると考えて解きます(そうじゃないと解けない)
頑張りましょう。
(1)解答・解説
まぁ、状態方程式ぐらいは書けると思いますので、試験でこの問題が出たら得点したいものです。
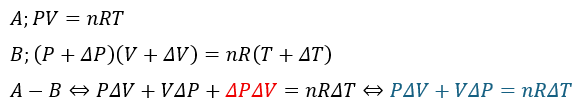
上の式の赤い部分は微小量の積なので無視して構いません(物理では微小量の積などのあまりにも小さいものはないものとして扱う近似を使える)。
青い部分が求めるべき関係式になります。
(2)解答・解説
(2)がこの問題で一番重い部分になります。
まぁ、この問題を解ければ自信を持っていいでしょう。
問題文にてPとVの比が一定なので(P/V=k⇔P=Vk)と表すことができます。
これはPがVの一次関数となっていて直線なので「系が外部にした仕事」を積分を用いずに表すことができます。
とりあえず、P-Vグラフを描いてみると。
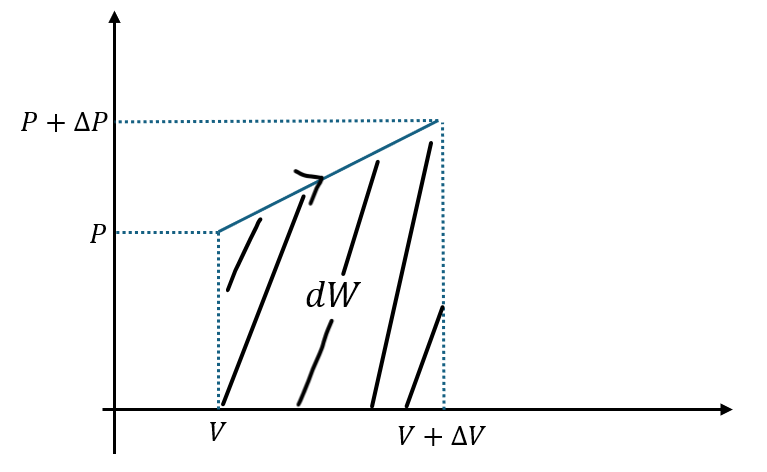
上の図の斜線部の面積が系が外部にした仕事になります(仮に膨張しているとします(ほんとは圧縮する。膨張しているので系が外部にした仕事は正)。
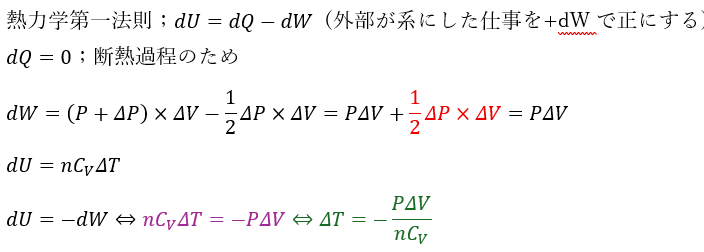
この緑の式をどうにかして変形したいと思いますが、ΔTがうっとうしいです。
ここで、(1)で導出した状態方程式に上の緑のΔTをそのまま代入します。
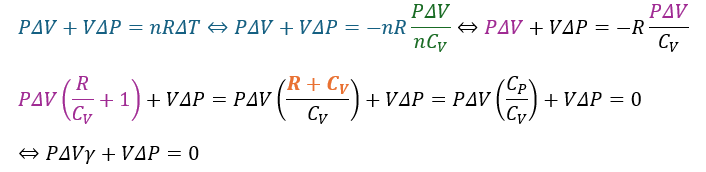
ここまで出来たら後はうまいこと変形するだけです。
- 青い部分・・・(1)で導出した式
- 緑の部分・・・熱力学第一法則で出した
- オレンジの部分・・・マイヤーの関係式
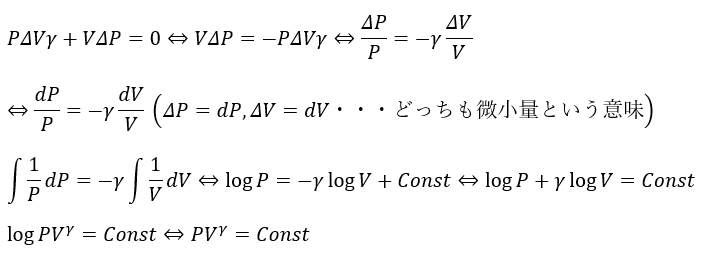
これでPとVに関するポアソンの公式を求めることができました。
問題はこれをTとVに関するポアソンの公式に変形したいのですが工夫します。
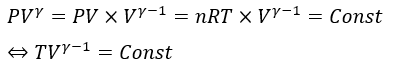
学生でよくT,Vのポアソンに公式を求められない人はいるので覚えといてください。



コメント