熱力学におけるエントロピーと問題の解説

こんにちは。Horyです。

今回の記事では熱力学のエントロピーについて解説すると共に、ちょっとした問題を解説します。

エントロピーは非常に難しい概念のため高校の熱力学では登場しません。そのため、読み飛ばしたい人は読み飛ばして構いません。

今回も頑張りましょう。

エントロピーって何なんだ？

エントロピーと言うと聞き覚えのない言葉のように思います。

理系の学生にこの質問をすると「エントロピーは乱雑さの度合い」を示すとかって答えます。

例えばですが・・・

上の説明は解釈的には正しいとは言えません。

エントロピーは熱力学(マクロ)と統計力学(ミクロ)で説明が違ってきます。

今回の記事では熱力学(マクロ)でのエントロピーについて説明していきます。

熱力学でのエントロピー
- 元に戻せない不可逆変化における変化の度合いを示す
- エントロピーの正負・・・変化の向き
- エントロピーの大きさ・・・変化の大きさ

非常に難しい概念のため、上の説明で間違っていたら申し訳ないです(専門書とか読んで色々考えてもこういう風にしか考えれませんでした)。

大雑把に言ってしまうと、「どの程度、熱を吸収・放出させて系を変化をさせましたか？」という指標だと僕は考えています。

熱力学におけるエントロピー微小変化(dS)は微小熱(dQ)と温度T(K)で以下のように定義できます(統計力学では別の式で定義する)。

イコールになるのは平衡状態と見なせる準静的変化のみです。

一般的にはTdS>dQとなります(一般的な変化は不可逆過程が多いから)。

これも難しいですが、具体的な意味を解説すると・・・

「系が熱量dQを受け取って起きるエントロピー変化というのは想定よりも大きい ⇔ 受け取った熱量以上に変化を残してしまう」というふうに考えてください。

また、問題では比熱c(不変)が与えられていてそれを使って問題を解くのが一般的かなと思います。

以下に示すのはエントロピー変化の問題で水がテーマの問題です。

この問題を例に解説します。頑張りましょう。

まぁ、比熱があるので、水についてはdQ=cdTとして変形させましょう。

熱源については、温度は変わりませんが、熱を与えていると考えてdS=dQ/TでdQは求めれます(熱の放出よりマイナス)。

問題の解答・解説です。

以上が解答になります。全体のエントロピー変化は計算してください。

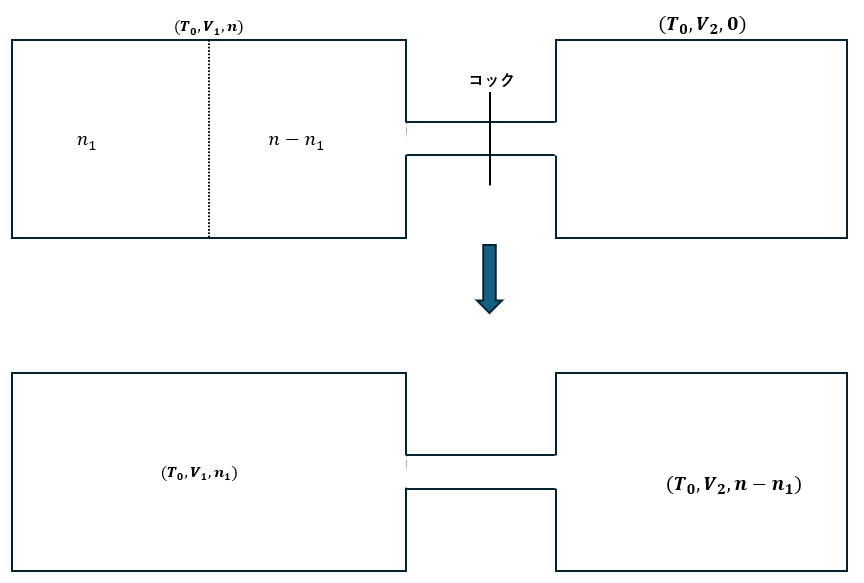
容器内に入った気体に関してエントロピー変化の問題を考えます。

上の図に示すように最初の状態から気体がn1[mol]の部分とn-n1[mol]の部分に分かれているモノとして考えます。

まずは、熱力学第一法則を考えます。ただ、ここに工夫が必要でdQ=TdSと変形してエントロピー変化が出るようにしないといけないです。

一応、注意点ですが、dQ=TdSとできるのは操作をゆっくりと準静的に行っているからというのは忘れないでください。

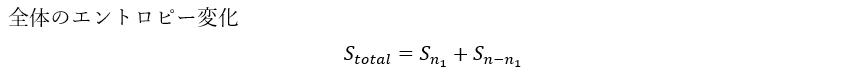
この問題について、本解説では熱力学的始点からエントロピーを定義して問題を解きましたが、この問題を統計力学的視点(ミクロ)から考えるとどうなるでしょうか・・・

結論を言うと答えは同じになります。まぁ、僕のやる気があればそのことに関する記事を書くかもしれません。