こんにちは。Horyです。
前回の記事では高校の化学で習得する気体法則をまとめました。
今回の記事では、混合気体と分圧に関してデス。基本的に、異なる気体を混ぜたときのそれぞれの気体の圧力(分圧)を求めたりする問題が多いです。
勘違いする人も結構多いのでそれらも含めて詳細に解説します。
今回も頑張りましょう。
混合気体について・・・
入試の現場では異なる気体を混ぜて計算する問題が出てきます。
混合気体を考えるときは2つの考え方があります。
- まとめて考える・・・モルがある→PV=nRT・・・面倒でミスしやすい
- 異なる気体で分けて考える
- 気体Ⅰだけで考える
- 気体Ⅱだけで考える
- 計算結果を統合する
ここで、異なる気体で考えるときに問題文に公開されている情報によって処理が分かれます。
- 圧力Pと温度T→それぞれの気体の占める体積
- 体積Vと温度T→それぞれの気体の圧力
個別に実演します。
気体の占める体積を求める
条件・・・容器の体積と混合気体の全圧、気体の物質量が判明していて、それぞれの気体の占める体積を求める。
- 体積VⅠの容器に気体Ⅰ
- 体積VⅡの容器に気体Ⅱ
- 混合気体の全圧をP
- 気体Ⅰは体積VⅠの部屋を占領
- 気体Ⅱは体積VⅡの部屋を占領
- VⅠ+VⅡ=V・・・容器を分ける
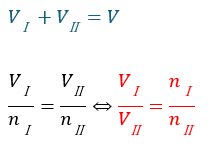
上の式の赤い部分が何で成り立つの?と思うかもしれませんが、アボガドロの法則を思い出してください。
「気体の体積と圧力Pが一定であれば気体の体積と物質量の比は一定になる」
上の青い式と赤い式を用いて各気体の体積を求めてみます。
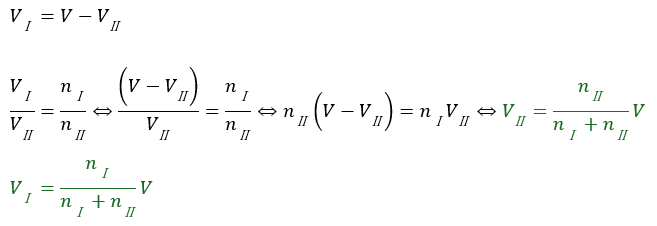
各気体の体積は物質量の比に依存することが分かります。
気体の分圧
条件・・・容器の体積と各気体の物質量、容器内の温度が判明しているとき、各気体の分圧を求める
- 気体ⅠはPⅠの圧力
- 気体ⅡはPⅡの圧力
- 混合気体の全圧はPⅠ+PⅡ=P
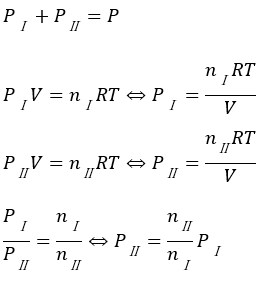
各気体について状態方程式が完成したので、混合気体全体で考えます。
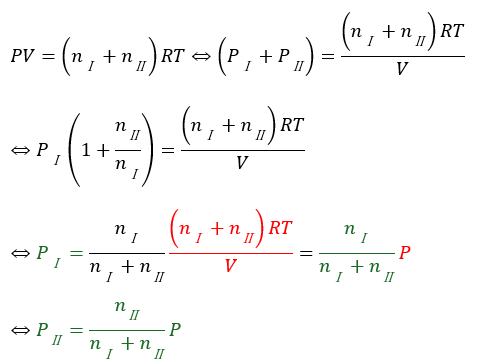
混合気体の分圧に関しても体積と同様に全物質量に対する割合になっていることが分かります。



コメント