こんにちは。Horyです。
前回の記事では波動の形をまとめると共に、正弦波に関して詳しく解説しました。
今回の記事は大学内容になりますが、フーリエ展開について解説しようと思います。
フーリエ展開は大学内容ですが、わかりやすく解説しようと思います。
フーリエ展開について・・・
フーリエ展開とは簡単に説明すると・・・
「グラフ上でどんなに複雑で煩雑な関数であっても、その関数に周期性が見いだせるのであれば、sinとcosの和で表すことが可能である」
もっと簡単に言うと、「周期関数を三角関数の級数として表すこと」がフーリエ展開です。
「そんな馬鹿な!」と思うかもしれませんが、本当です。
パラメーターを以下のように設定します。
- 周期関数;f(x)
- 周期;2L
- An;係数
- Bn;係数
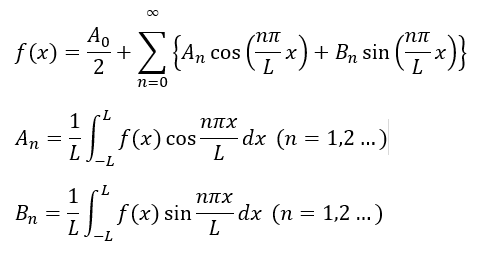
上の式を見ると周期関数の周期と係数AnとBnさえ決めることが出来ればどんな周期関数でも関数で表せると言うことです。
(何で上のように表せるかという解説はこの記事ではやりません)
以下では係数を求めてみます。
下準備;偶感数と奇関数
下準備として偶感数と奇関数について考えます。
- Sin;奇関数 (原点について対称)
- Cos;偶感数 (y軸について対称)
- 「偶感数と奇関数の積」=「奇関数」
- 「偶関数と偶関数の積」=「偶感数」
- 「奇関数と奇関数の積」=「偶関数」
上のことが成立するので・・・m,nが正整数であると考えると・・・
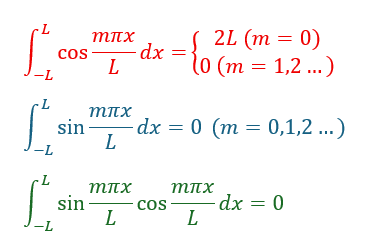
上のことが成立します。
また、三角関数の積の積分について以下のことが成立します。
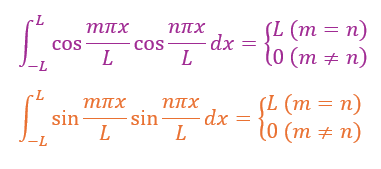
係数Anを求めてみる
まぁ、結構複雑なことをやるのですが。。。
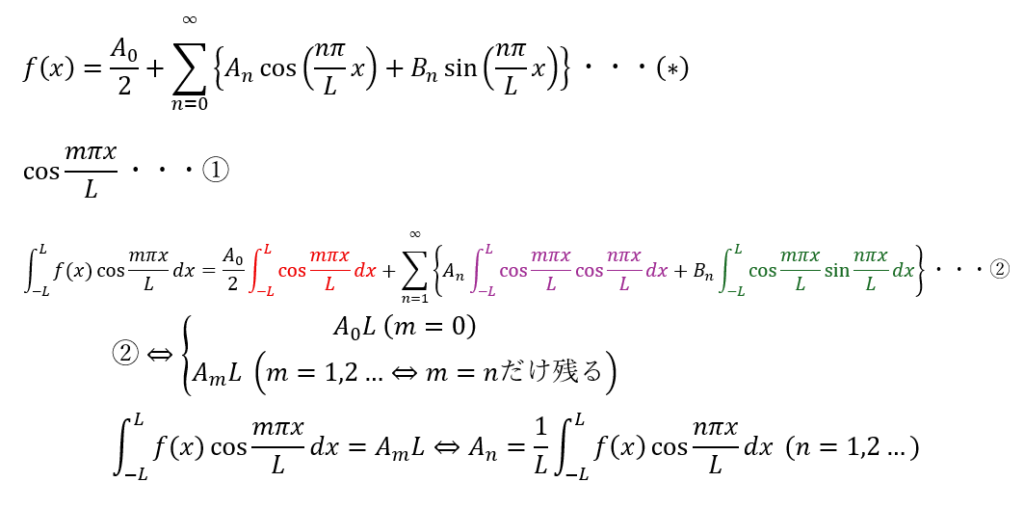
係数Bnを求めてみる
さっきと同じ要領で求めてみます。
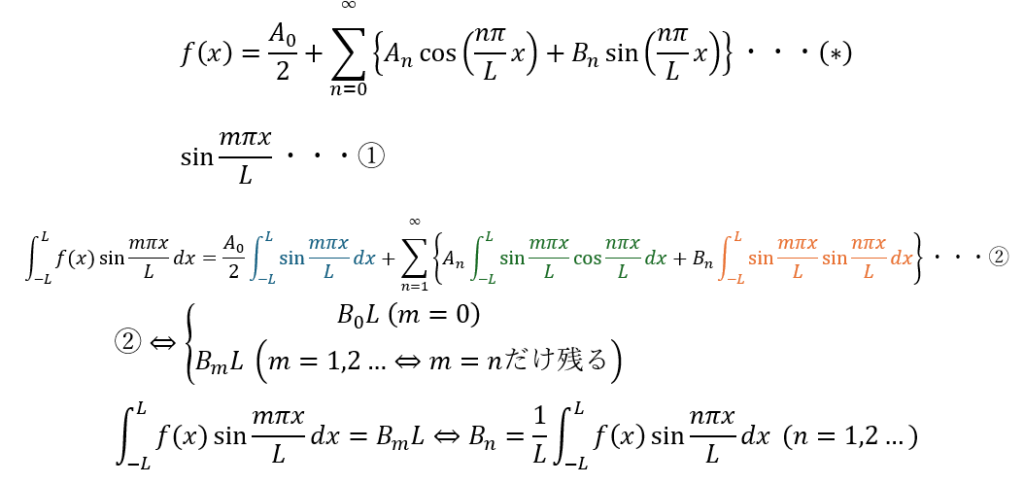
フーリエ展開の実践
先ほど、どのように複雑な関数でもsinとcosの級数で表せると話したので実際にやってみます。
以下のような関数を考えます。
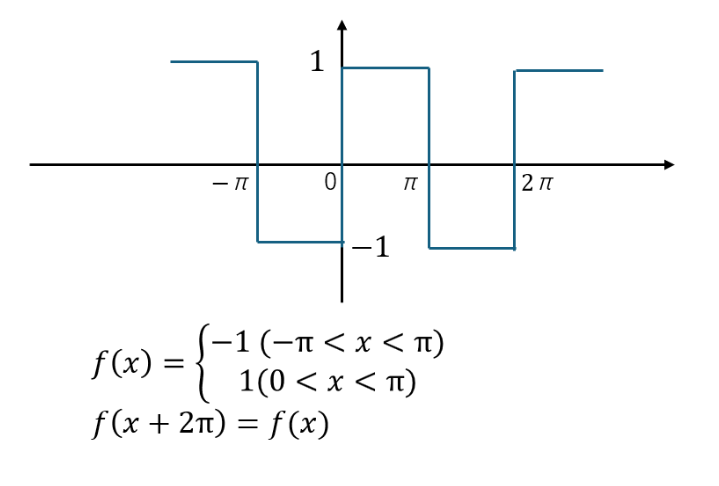
まぁ、計算は省略しますが、係数を求めていきます。
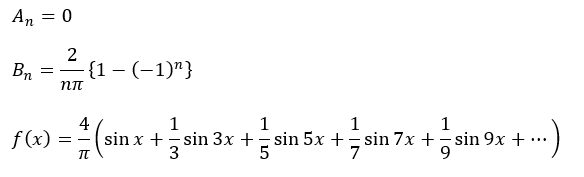
グラフに示します。①→⑥へと番号が増えるに従って級数の数が多くなります。
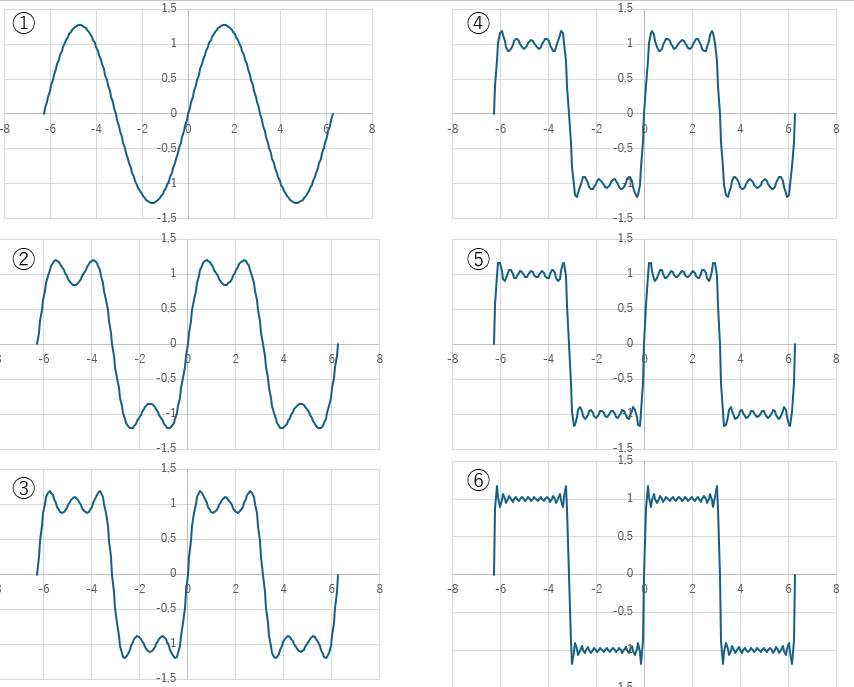
級数の数が多くなればなるほどグラフは問題の周期関数に近づきます。
このように、フーリエ展開を使えば、どんな複雑な関数でも周期的であれば三角関数の級数で表すことが出来ます。
これが日常生活のどこで応用されているのかというとスピーカーのノイズキャンセルとかに応用されています。
(特定の方向にしか音が聞こえないようにする⇔音を出したくない方向の音波を三角関数で表して重ね合わせにより音波を相殺する)



コメント