こんにちは。Horyです。
前回は固体の溶解度をテーマにして溶解度曲線や実践問題への対処法に焦点を当てて解説しました。
固体だけでなく気体にも溶解度というのはあります。
今回の記事では、気体の溶解度について簡単に解説するとともに、受験生の皆さんが混乱するであろうヘンリーの法則に関して簡単に解説します。
今回も頑張りましょう。
気体の溶解度
溶質が溶けるプロセスでも話しましたが、「溶ける」とは溶質分子が溶媒分子の引力に引かれて、溶媒分子の間に入り込むことです。
これと同じようなことが気体でも起こって、気体では二通りの溶け方があります。
- ①;気体分子と水の化学反応→親水性イオン→化学溶解
- ②;気体分子が分子間力で水和→物理溶解
化学溶解を起こす物質はアンモニア(NH3)と塩酸(HCl)になります(中学校の実験でアンモニアと塩酸がめっちゃ水に溶けたことを覚えていますか?)。
化学反応式で示すと・・・
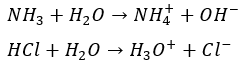
- アンモニアに水・・・アンモニウムイオンと水酸化物イオン
- 塩酸に水・・・オキソニウムイオンと塩素イオン
このように水との化学反応でイオンになって、イオンが水と非常に相性が良いので溶けます。
一方で、高校化学では、上の二つ以外の物質は水に物理溶解すると考えればいいです。
ヘンリーの法則
受験生の多くが混乱することになるヘンリーの法則です。
ヘンリーの法則とは、「物理溶解する気体の水への溶解度はある値までは気体の分圧に比例する」という法則です。
これを式に表すと・・・

押す力ってどういうこと?って思うかもしれませんが、例を出して示すと・・・
- ピストン内に水と気体
- ピストンを押すと体積が減る
- 体積が減ると気体の圧力が増える
- 気体の分圧も増加する
これは、押す力をx倍にすると水にx倍溶けるということを意味します。何度も言いますが、水に溶けにくい気体で成立する法則です。
ヘンリーの法則 証明
一応、気体Xを仮定して考えてみます。
水に溶けているXと気体のXに以下の式で示す平衡関係が成立しているとします。

ここで、水に溶けていない気体Xについて個別に状態方程式を立てます。
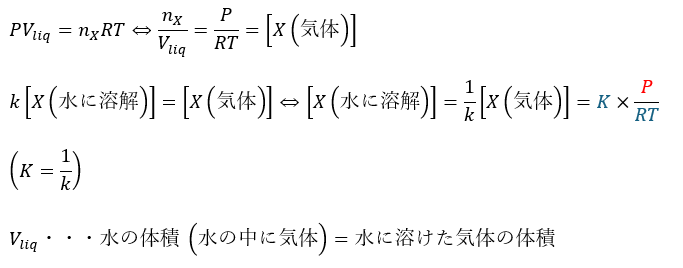
- 赤い部分・・・変数
- 青い部分・・・定数
上の式を見ると確かに水に溶けるXの量は圧力に比例することが分かります。
ここで、ヘンリー定数kが温度により変化するといいましたが・・・
- 水の温度上昇
- 粒子の熱運動による運動エネルギー増加
- 分子間力による水和を断ち切る
- だから、水の昇温で気体の溶解度は減少!
溶ける量は体積か物質量のどっちだ?
ここで、受験生の皆さんが一番疑問に思っていることを書きます。
「ヘンリーの法則の問題では気体の溶ける量を体積で書いているけど、物質量とか別の方法もあるんじゃないの・・・」と言うことです。
何で体積(mL)とかで書いているのかというと「ヘンリーの法則の発見当時」は「物質量」という量の定義がありませんでした。
だから、水に溶ける量を溶ける前の体積で仕方なく表したのです。
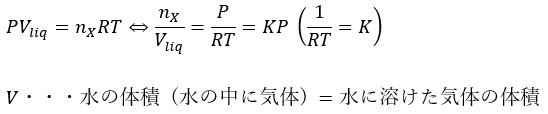
溶けている量を体積(mL)で表すとして、圧力を2倍にすると溶ける物質量も2倍になります。
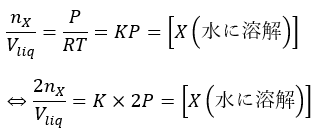
気体の状態方程式「PV=nRT」でも分かると思いますが、溶ける量を「体積(mL)」で表すと、圧力を何倍にしても溶けている体積は一定になります(ただし、これは押していた圧力と同じ圧力をかけて水に溶けている量を取り出した場合で、標準状態に戻すと普通に2倍になります)。」
これがヘンリーの法則で多くの受験生が混乱する理由です。だから、紛らわしくないように溶ける量は物質量(mol)で表しましょう。

非常に分かりにくい内容かと思うので図も示します。
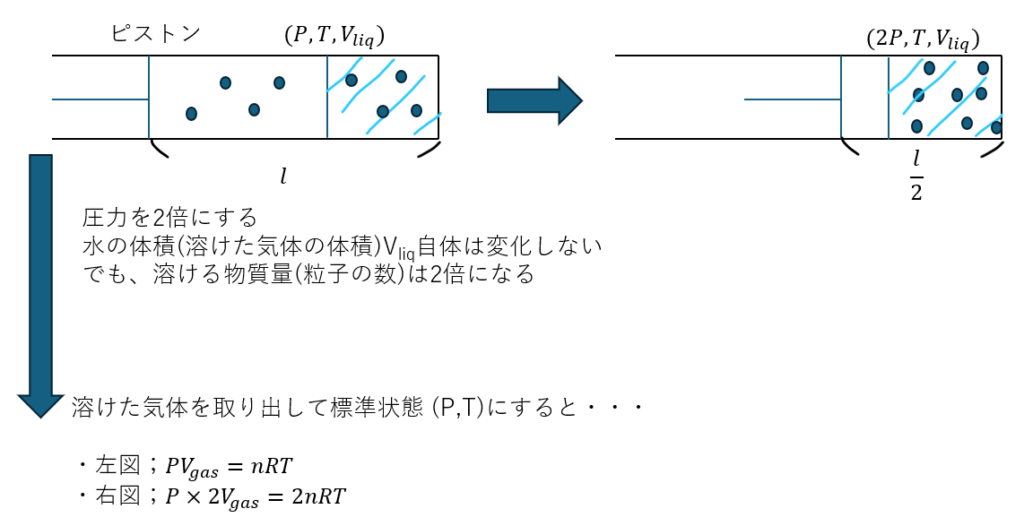
問題で意識しなければならないことは以下の3つです。
- 溶ける気体の体積は標準状態での体積か?
- 溶けている気体の体積は容器内の状態での体積か?
- 必ず物質量で考えて体積に変換すること
演習問題への応用
演習問題へどのように応用するかを以下の2つの手順を用いて解説します。
- ①;ヘンリー定数Kを求める
- ②;ヘンリー定数から問題を解く
例えばですが、問題で水温T℃、水1Lに標準状態でV1L溶けるとします。「標準状態」という言葉が出ました。大事です。
必ず、下の公式から入ってください。
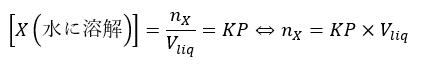
上の式に標準状態での気体の状態を当てはめます(標準状態は気体で1mol 22.4L、だから、物質量から求めれる。
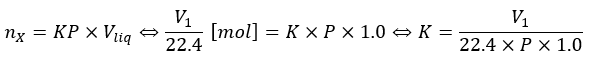
そして、①を用いて、例えば、T1℃で水2Lに2Pの圧力で溶ける量とかを「物質量」で求めるなら・・・
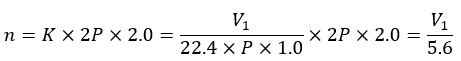
水に溶けているときの気体の体積はV1で変わりません。物質量を質量に変えたりすれば後は分かりますよね。
ちなみに、これを標準状態で取り出した場合、気体の体積はV1の4倍になります。図を見て考えれば当たり前ですよね。



コメント