こんにちは。Horyです。
今回の記事で紹介するのは図形の問題で正方形に内接する円と三角形の問題です。
具体的には三角形の頂点を正方形の頂点に固定し、残りの2点は円周内を動くとしたときに三角形の面積の最大値を求める問題に取り組みます。
今回も頑張りましょう。
正方形に内接する円と三角形の面積
以下の図形を考えます。
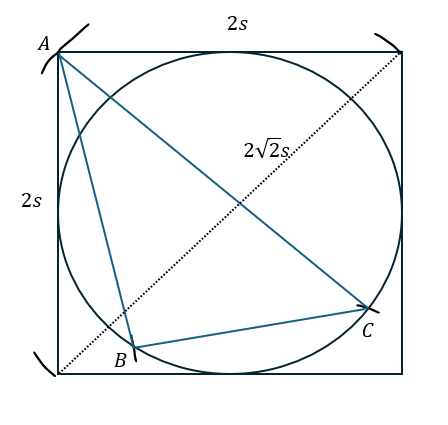
- 点A;固定する
- 点B,C;円周を自由に動くが互いに異なる
- 三角形ABCの面積
- 正方形の一辺の長さは円の半径の2倍
どこかで話したことがあるかもしれませんが、図形問題は基本的に3つのことが利用できます。
- 三角比 (三角関数)
- 座標
- ベクトル
今回であれば、自分の都合の良いように「座標設定」⇒「三角関数」が望ましいです。
また、さすがにしつこいと思いますが図形量の問題では辺or角のどちらを変数にするかです。
今回であれば正方形の一辺は分かっています。
どこかの角度をθと置けば辺をθで表せそうです。
都合の良い座標を設定
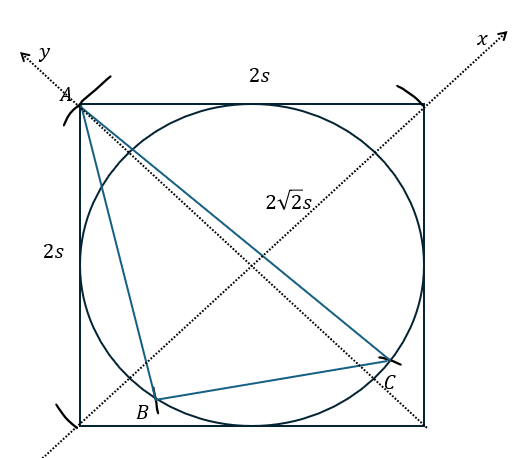
上のように座標軸を設定します。

予想を立てる
数学が出来ないやつは予想を立てずに突っ走ります。
数学が出来るやつは先に検討を立てます。
今回の問題であればBとCが動きます。
ということは、BとCの場所によって辺BCの長さに無限の組合わせが存在し収拾がつかなくなります。
そのためBCの長さを固定して面積が最大となる時を予測します。
DはAからBCに下ろした垂線の足とします。
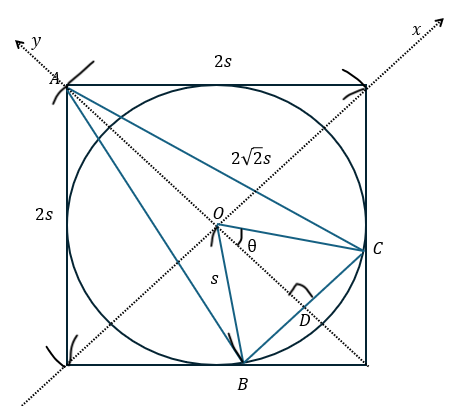
まぁ、図を用いて考えてみれば分かりますが(PQの長さを固定して動かす)、ABCの面積が最大となるのはBCとx軸が平行になるときです(y軸と垂直)。
三角形の面積を求めてみます。
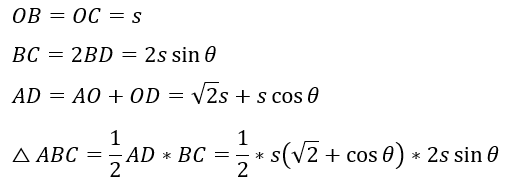
BCの長さを変化 (θの変化)
BCの長さの最大値と最小値を考えてみましょう。
- BCの範囲;0 <BC ≦2s(直径) ⇔ 0< θ< 90°
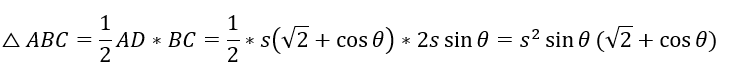
基本的にsinやcosは奇数乗であれば統一できません(数ⅠAⅡBでは無理)。
そのため、ルートで二乗の形を無理矢理作ってsinとcosを偶数乗にします。
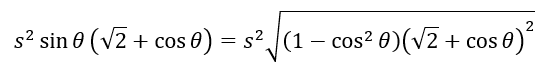
後はcosθ=tとおいてルートの中を微分してください。
自学自習してください。
この問題も本質的には三角関数の予選・決勝法だったんですね。
追加問題;円内を動く三角形
追加問題です。
以下の図形を考えます。
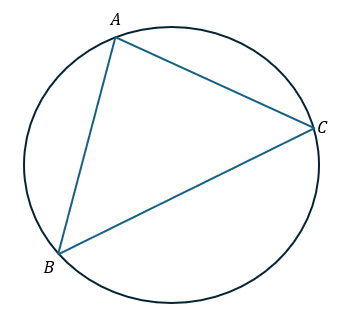
- 半径2の円
- 円周上に異なる3点A,B,C
- A,B,Cが動くときの△ABCの面積の最大値
これは自分でやってみてほしいですが考え方は先ほどと全く同じです。
- 3点が独立で動く⇒収拾がつかない
- Aを固定する
- BCの取り方で長さが無限の組合わせ
- BCの長さを固定
- ⇒どんなときに最大をとる?
- ⇒さっきと同じ
頑張ってみてほしいです。



コメント