こんにちは。Horyです。
前回の記事では正弦波について詳細を解説しました。
今回の記事では一次元進行波(正弦波)の問題に取り組もうと思います。
波動における最も基本的な問題になるので是非理解していただきたいです。
今回も頑張りましょう。
一次元進行波 (横波)
一次元進行波の問題は横波と縦波の場合があって、最初は横波の問題を解こうと思います。
以下に示すのは問題になります。

この問題を例に解説します。
一応、復習を行うと共に、事前準備を行いたいと思います。
- 力学的波動・・・弦の振動/音波/水面/波 (運動方程式が原理)
- 光学的波動・・・電磁波 (マクスウェル方程式が原理)
- 波動・・・振動が媒質や空間を伝わっていく現象
最も簡単な波動の模型は弦の振動です。なので、この問題は弦の振動を取り扱っているモノとします。
無限に長い弦を考えて反射を考えないモノとします。
(1)解答・解説
(1)の解答・解説になります。
原点のみを切り取ってみると、弦は以下の式のように振動しています。
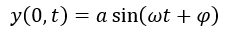
ここで、ωは角振動数であると考えます。
「y(x,t)を求めろ」・・・y(0,t)において位置xだけ離れたところの弦の変化を求めろ
のように言い換えることが出来ます。
ここで、位相速度をCとします。
時刻が(t,x)での弦の変化というのは(t-x/c,0)での弦の変化に等しいです。なので・・・
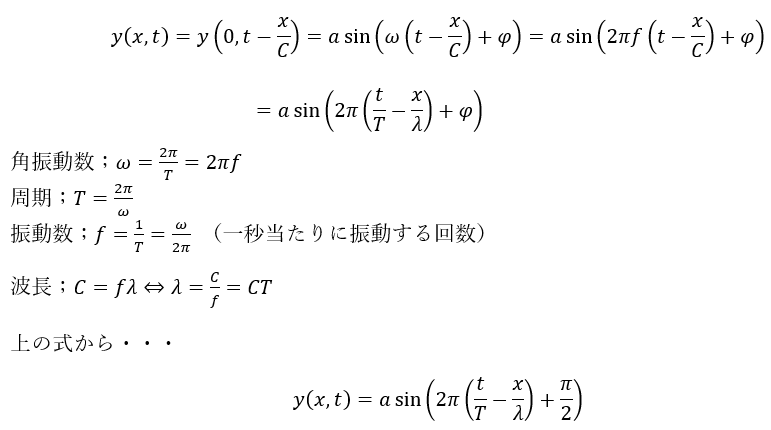
以上が(x,t)における媒質の変位になります。
(2)解答・解説
(2)の解答・解説になります。
時刻がt=T/4の時が弦のどこの変位であるのかを考えます。
時刻をy(x,t)の式に当てはめてみます。
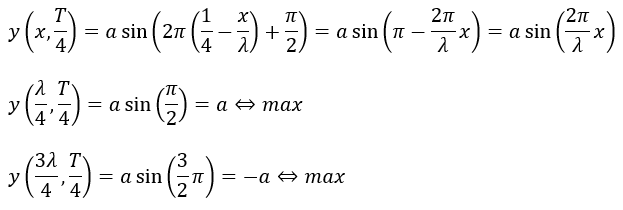
以上が変位の大きさの最大値になります。
一方で速度の最大値ですが、微分を使えば楽勝です。
ただし、注意しなければならないこととして、「媒質の動きの速さ=v」と言うのは「波の伝わる速さ(位相速度)=C」ではありません。
今回求める「媒質の動きの速さ」というのは位置を微分して求めます。
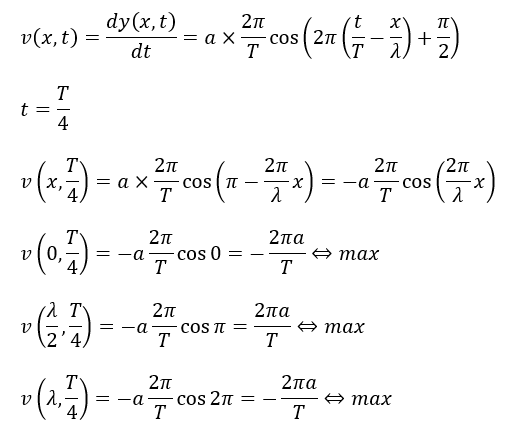
以上が解答になります。
加速度に関しても速度を微分すれば良いだけです。
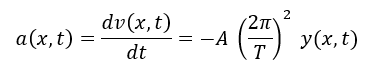
このようになるので、変位を最大にする点が加速度を最大にします。
一次元進行波 (縦波)
縦波の問題を考えてみます。以下は問題です。

この問題を例に解説します。問題を解く前におさらいです。
- 横波・・・波の進行方向に垂直な方向に媒質が移動する波
- 縦波・・・波の進行方向に平行な方向に媒質が移動する波
気体や液体などの流体中を伝わる波は縦波のみです。一方で固体は縦波と横波ともに伝わります。
そして、縦波について、疎な部分と密な部分を考えると・・・
(1)解答・解説
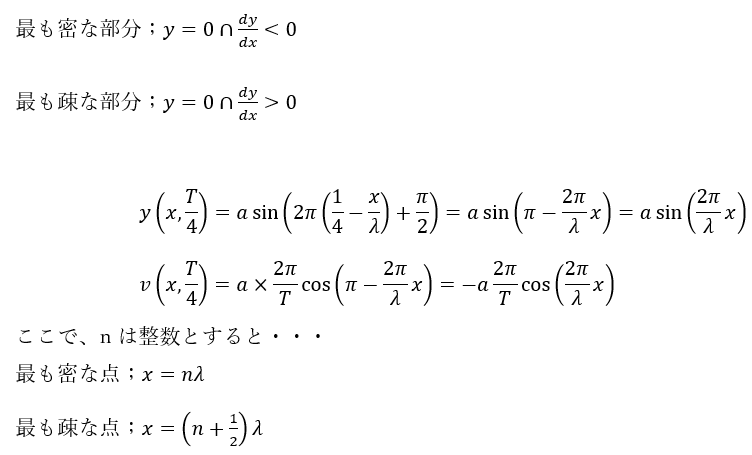
(2)解答・解説
問題は任意の時刻における媒質が最も疎になっている点です。
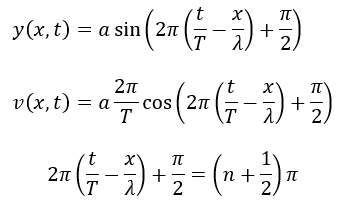
これをxについて解けば答えになります。



コメント