こんにちは。Horyです。
今回の記事も場合の数に関する問題になります。
皆さんは格子点という言葉をご存じでしょうか?
格子点とは座標平面(空間)において、xもyの値も整数で表される点のことです。
格子点の数を数える問題などは学生が非常に嫌がる分野でもあります。
今回は格子点を用いる場合の数の問題を解いていきます。
今回も頑張りましょう。
格子点と場合の数
以下に示すのはこの記事で取り組む問題になります。

この問題を例に解説します。
この問題は座標平面を用いて格子点を有効活用するのが効果的です。
(1)解答・解説
各製品をX,Y,Zとしてそれぞれの製造数をx,y,z(自然数)とします。
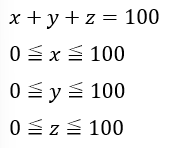
とりあえず、文字が3つだとやりにくいのでz=kとして固定しましょう(文字が複数出てきたら一つを固定して変数を減らすのは重要な考え方です)。
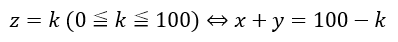
- 上の式は直線
- 傾き;-1
- 切片;100-k
これを座標平面に置き換えてみます。
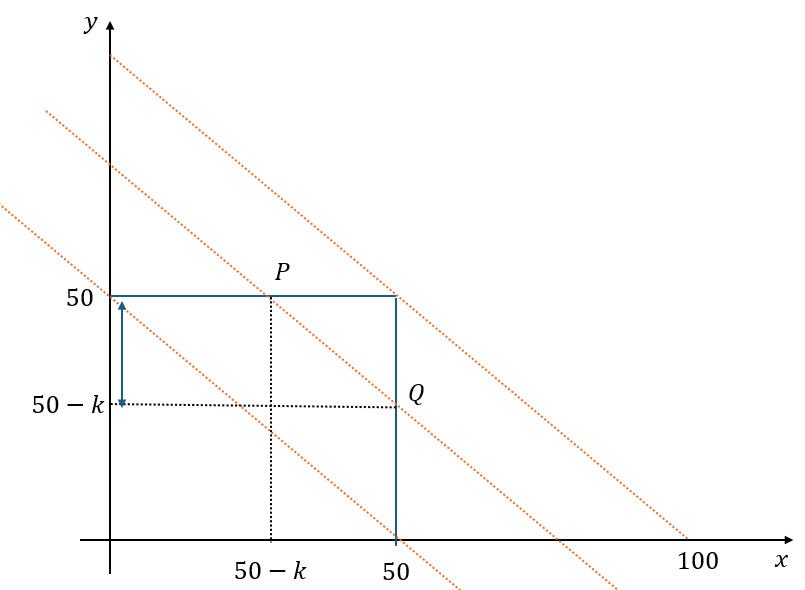
青い正方形の中の格子点の総数が本問の答えです。
上の図のオレンジの点線がx+y=100-kです。kの値によって様々な線になりますが・・・
組(x,y)は上図の線分PQ上の格子点と1対1対応することが分かります。
線分PQ上の格子点の数を求めると・・・
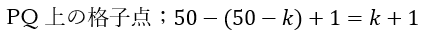
結局、格子点の数はPのy座標とQのy座標の間の整数の数に対応します(まぁ、考えてみれば当たり前)。
これを、k=0~50まで足せば青い正方形の中の格子点の数を全て求めれます。
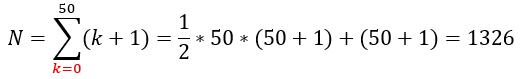
以上が解答になります。
(2)解答・解説
本問から難易度が跳ね上がります。
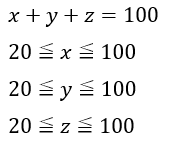
文字が3つもあって面倒なので先ほどと同様にz=kとして固定します。
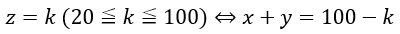
先ほどと同様に座標平面に示します。ただし、範囲の下限には気を付けましょう。
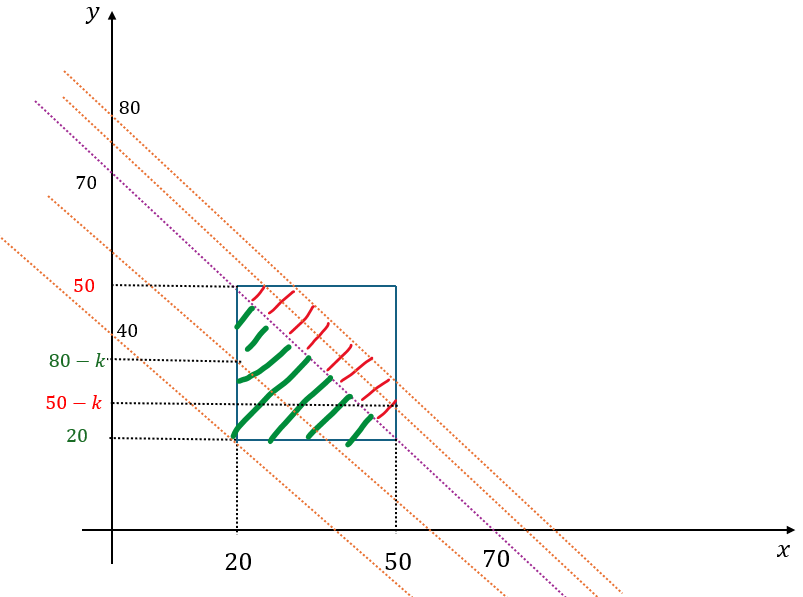
この問題は図の赤い斜線部と緑の斜線部で格子点の数え方が異なってきます。
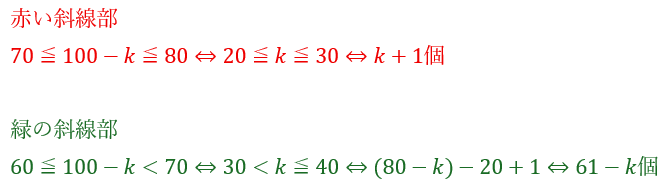
- 赤の不等式について
- 下限が20の理由 ⇔ kの数が20個以上だから
- 上限が30の理由 ⇔ 境界線
- 緑の不等式について
- 下限が30の理由 ⇔ 境界線
- 上限が40の理由⇔ k>60だとx,yのどちらかが20未満になる
後はΣを用いて足し算をしていけばいいだけです。
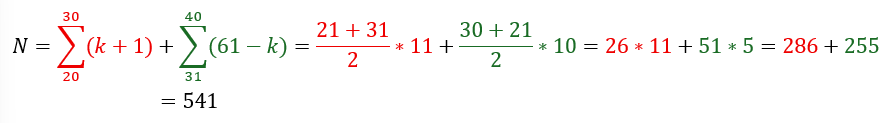



コメント