こんにちは。Horyです。
今日も整数問題について解説しようと思います。
今回の問題は任意の値段と組合わせの問題に関してです。
この問題も内容がシンプルで有名ではありますが、いざ、問題を解くとなると解法がなかなか思いつかない人が多いです。
今回はそのような問題の解説を行いたいと思います。
今回も頑張りましょう。
問題 任意の値段と組合わせ
以下に示すのは今回の記事で取り組む問題になります。
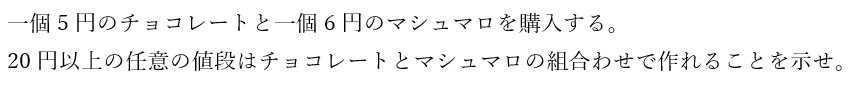
この問題に取り組みます。
ただし、注意として、「チョコレートだけ購入する」とか「マシュマロだけ購入する」という状況もありと見なします。
この問題ですが、問題内容は非常にシンプルですが、学生に出題すると手が止まりがちです。
重要なのは「余りに注目すること」と、特定の数に注目したときに、全ての整数(自然数)は適当な文字と余りを用いて表せるということです。
このような場合は「何円以上」の「何円」がどの数の倍数になっているかに注目するのがポイントです。
もし、「何円」が問題文のどの数の倍数でもなければ、「何円」より少し小さいor大きい数で倍数になっているものに焦点を当てます(まぁ、小さい数に注目した方が楽)。
今回は「20円」が5の倍数なので5に注目します。
kを0以上の整数として、5に注目したとき、0以上の全ての整数は以下のように表せます。
- 5k・・・5の倍数
- 5k+1・・・5で割って1余る数
- 5k+2・・・5で割って2余る数
- 5k+3・・・5で割って3余る数
- 5k+4・・・5で割って4余る数
以上から全ての整数を上のように分けて表すことが出来ました。
このことがポイントになります。
解答・解説
問題の解答・解説になります。
この問題は5円のチョコと6円のマシュマロの組合わせにおいて「最低額を20円として、21~24円を作ることができるか?」と言い換えることが出来ます。
実際にやってみます。
- チョコ4個・・・5×4=20円
- チョコ3個+マシュマロ1個・・・5×3+6×1=21円
- チョコ2個+マシュマロ2個・・・5×2+6×2=22円
- チョコ1個+マシュマロ3個・・・5×1+6×3=23円
- マシュマロ4個・・・6×4=24円
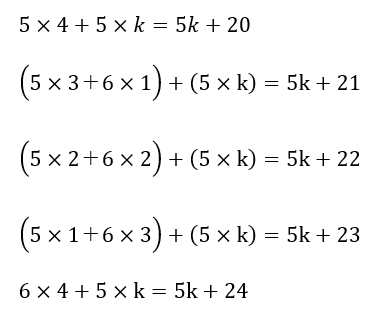
上の5数は全てが20円以上の連続する自然数になります。
Kを任意に変えてあげれば20円以上の全ての値段の組合わせが完成します。



コメント