こんにちは。Horyです。
今回の記事も整式の割り算に関する記事を書こうと思います。
私たちは、余りや割る整式の情報から割られる整式を特定する問題には取り組んだことがあると思います。
一方で、整式が無限個存在することを証明する問題は馴染みがないのではないのでしょうか?
今回はそんな問題に取り組もうと思います。
今回も頑張りましょう。
整式が無数に存在することの証明
以下に示すのは整式が無数に存在することを証明する問題です。
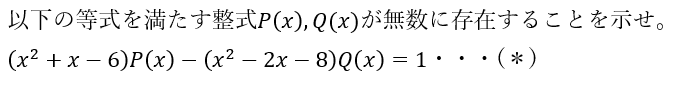
この問題を例に取り組みます。
非常に難しい問題ですが頑張りましょう。
無限個あることの証明
- 無限個あることの証明
- 直接的・・・1つ求めればよい
- 間接的・・・背理法や帰納法
- 多項式の等式
- 次数、係数が全て等しい (恒等式)
- 数値代入法 (十分性の確認に注意)
ところで、無限個あることの証明なんてできるわけねーじゃん!と思うかもしれませんが普通にやってもできません。
工夫することでなんとかできるようになります。
ところで、私たちが考える整式P(x)やQ(x)は何次式でしょうか?
数学ができない奴は次数を闇雲にあてはめます。
無限個の存在を示すポイントとして条件を満たす系列を作ることから始めるのが得策です。
今回であれば簡単のために条件を満たす一次式の系列を作ります。

これで下準備は完了です。
一次式を1つ求める
まずは一次式を1つ求めてみましょう。

計算はめんどくさいカモですがこれぐらいはできてください(後で通分をラクにするためにあえて約分はしていません)。
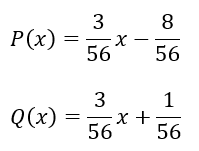
以上から一次式の具体例を1つ求めることができました。
ただし、これで終わってはダメで元の式に代入して十分性を確認しましょう。
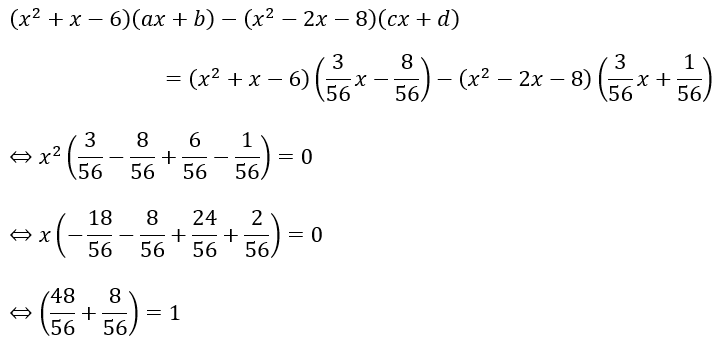
別解;剰余の定理
上の解答では具体的な一次式を1つ求めましたが、別解として剰余の定理を用いる方法があります。
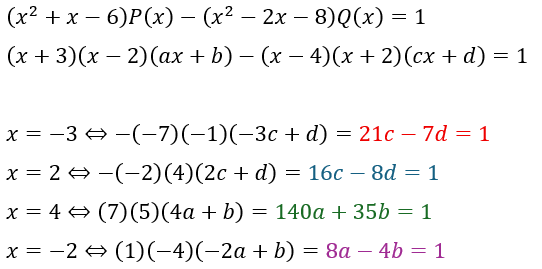
こっちの方が簡単かもしれませんね。
無限個あることの証明
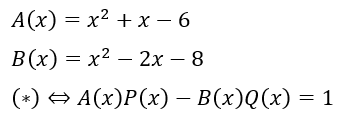
ここで、先ほど求めたP(x)とQ(x)の具体例をそれぞれP0(x)とQ0(x)と置きます。
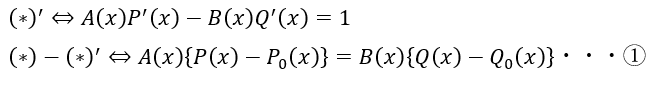
ここで、R(x)を任意の多項式と考えます。
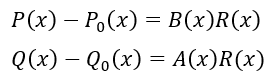
これは①に代入しても成立します。ということは・・・
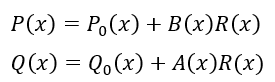
R(x)を多項式として任意に変えても上の式は成立します。
そのため、上で求めた具体的な一次式を起点として無限個の多項式P(x)とQ(x)が作れるので無限個存在することが示されました。



コメント