こんにちは。Horyです。
複素数平面も終わり、私の高校数学の記事の最期の分野になる数Cの二次曲線に突入しました。
今回の記事では放物線の性質について、原理と本質の理解を目的に記事を書きたいと思います。
数学Ⅰでも放物線については習ったと思いますが、数学Cではより深く放物線について掘り下げたいと思います。
今回も頑張りましょう。
数学における放物線の定義
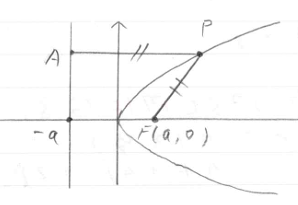
まず、数学における放物線とは「定点FとFを通らない直線lからの距離が等しい点の集合」のことです。
- 定点F・・・焦点
- 直線l・・・準線
放物線の式は以下のように表せます。

実際に①のグラフを以下に示します。
放物線の方程式の証明
以下に放物線①の方程式を導出してみます。
放物線は「定点FとFを通らない直線lからの距離が等しい点の集合」です。だから、上で示した図において、「PA=PF」が成立します。
- P・・・放物線上の任意の点;(x,y)
- A・・・Pから準線lにおろした垂線の足;(-a,y)
- F・・・放物線の焦点;(a,0)
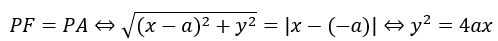
以上から確かに上で示した方程式が導出できます。
放物線の接線
放物線の接線についてです。①で示した放物線の接線を求めてみます。
微積分で話した陰関数の微分が使えそうですね。
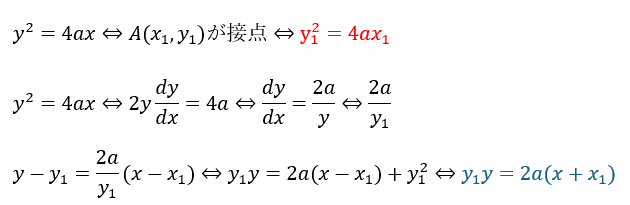
上の式の青い部分が放物線の接線公式です。
放物線 基本問題
以下に示すのは放物線の基本問題です。基本問題なので必ずできるようになってください。

このような問題に取り組むときは以下のことを意識します。
- 基本形を求める・・・上に示した①か②の形にする
- 題意の放物線が基本形をどの程度平行移動したものかを考える
- 基本形の焦点や準線を求める
- 基本形の焦点や準線を平行移動
この二点を意識しましょう。
問題 解答・解説
問題の解答・解説です。基本形は以下の形です。
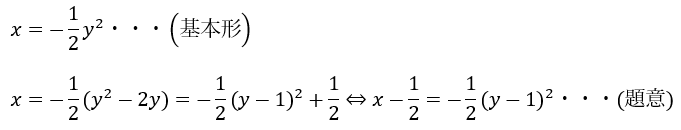
上の二つを比較するとこの放物線は基本形を「x軸に-1/2」・「y軸に-1」だけ平行移動したものです。
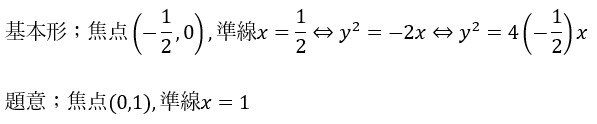



コメント