放物線の応用問題 放物線と焦点を通る直線

こんにちは。Horyです。

今回の記事では放物線に関する応用問題に取り組みます。

放物線の基本性質に関する記事はこちらなので事前に読んでおくことをお勧めします。

放物線と放物線の焦点を通る直線には面白い性質があるので今回はそのことについて記事で触れようと思います。

今回も頑張りましょう。

放物線と焦点を通る直線

以下に示すのは放物線と焦点を通る直線に関する問題です。

この問題を例に取り組みたいと思います。

放物線の性質を思い出してください。焦点はF(p,0)になります。また、状況を以下に図示します。

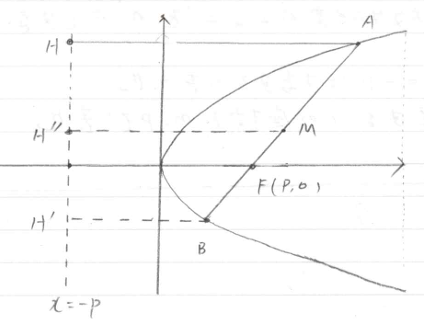
円が準線に接することを証明します。この問題の手順を示します。

この3ステップで問題を解こうと思います。

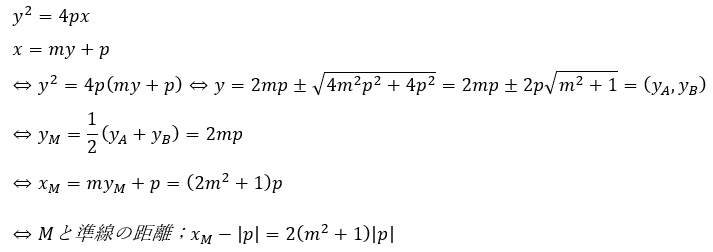
これにより線分ABの中点Mの座標を求めると共に、中点と準線の距離を求めれました、これが線分ABの半分の長さになれば勝利です。

次に、ABの半分の長さを求めます。

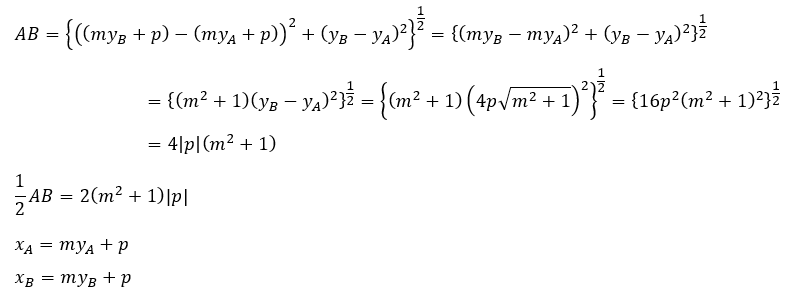
以上から、ABの中点Mと準線の距離と線分ABの半分の長さが同じ値を取ったのでABを直径とする円は準線に接することが分かりました。

直線の直交を示します。２つの直線の傾きの積が-1となれば良いです。

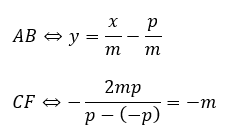
以上より、傾きの積が-1になったので直交します。