こんにちは。Horyです。
今回の記事では座標平面上での2物体の衝突について、ビリヤードを例に考えてみたいと思います。
この記事は以下の記事を読んでいることが前提となる記事なのでまだの人は読んでおいてください。
- 線積分と物体がされる仕事 原理と本質の理解
- 保存力と位置エネルギー 原理と本質の理解
- エネルギー保存則について 原理と本質の理解
- 力積と運動量について 原理と本質の理解
- 重心速度一定の法則 原理と本質の理解
- 2物体の衝突 保存則と反発係数
今回も頑張りましょう。
ビリヤードでの2球の衝突
以下に示すのはビリヤードにおける2球の衝突問題です。

この問題を例に解説します。
分かりやすいように以下に状況を図示します。
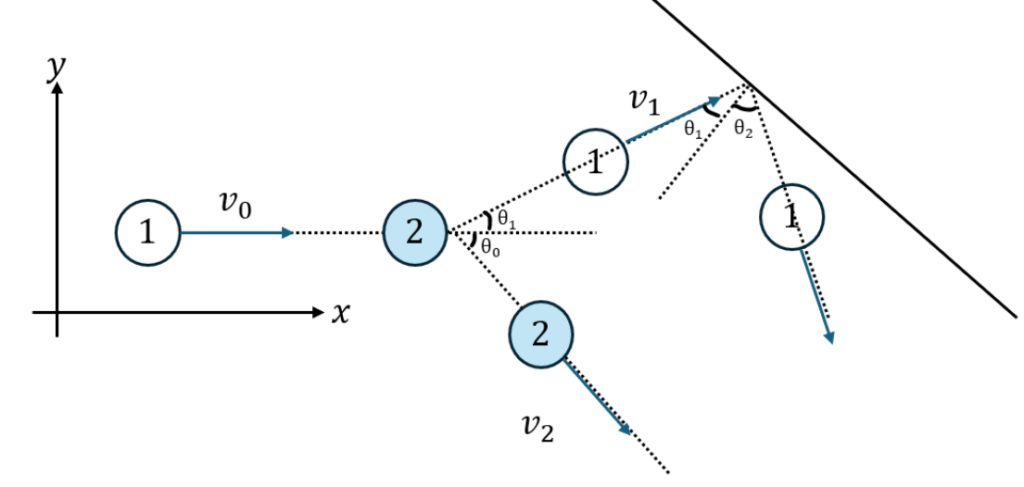
問題文で速さとなっていることに注意です。
速さはベクトル量ではなくスカラー量です。運動量保存則については成分ごとに分けて書く必要があります。
また、反発係数eが1ではないですが、問題文では弾性衝突とみなしているのでエネルギーは保存します。
(1)・(2)解答・解説
(1)と(2)の解答・解説です。
まずは、速度ベクトルを表してみます。
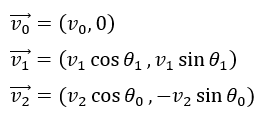
運動量保存則を成分ごとに記述します。
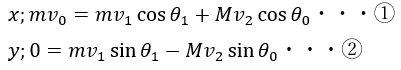
また、弾性衝突よりエネルギーは保存します。
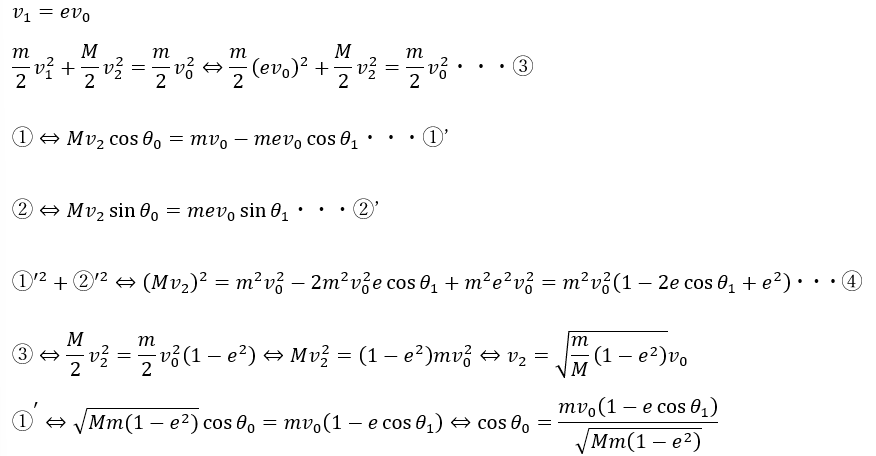
(3)・(4)解答・解説
球同士の衝突の反発係数や角度についての情報が分かったので代入して情報を整理します。
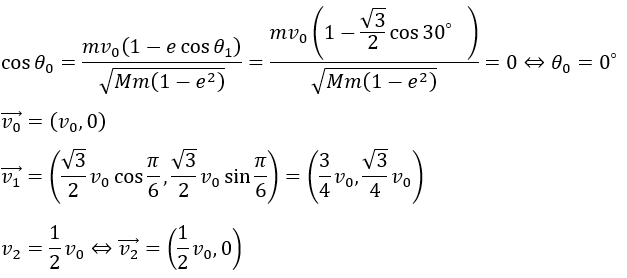
球の衝突時に球①が球②より受けた力積の大きさは球②の運動量変化の大きさに等しいです。よって・・・
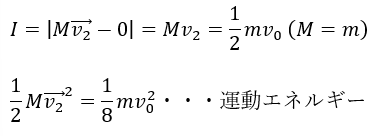
以上が解答になります。
(5)~(7)壁との衝突
以下に示すような座標を取ります。
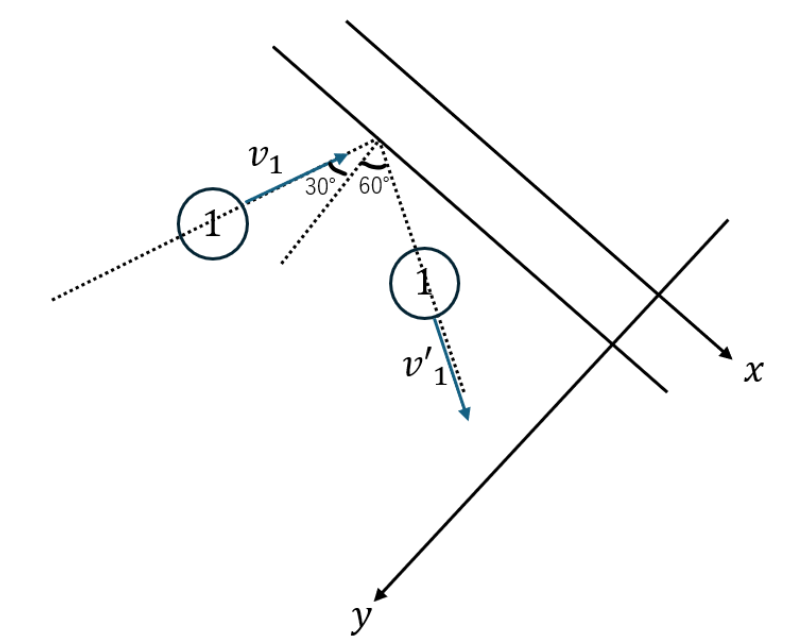
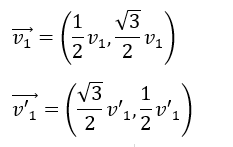
ここで、壁が球①に与える抗力は壁に垂直な成分のみです。
だから、壁に衝突前と衝突後でx成分の速度は変わりません。つまり、跳ね返り係数を考えるときはy成分の速度を比較して求めればよいです。
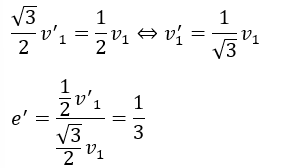
そして、求める力積の大きさは運動量の壁に垂直な方向の変化に等しいので・・・
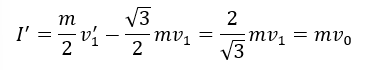
また、衝突により失ったエネルギーは・・・
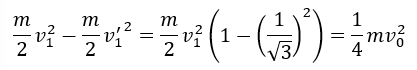
ここで、注意してほしいのが、壁と球①の衝突は弾性衝突ではないです。実際にエネルギーは保存していないためです。
そもそも、「e=1」でないとエネルギーは保存しませんが・・・「e≠1」でも、問題によっては弾性衝突とみなしてエネルギー保存則を近似的とする場合があります(そうじゃないと解けない)。
今回の問題では・・・
- 球①と球②の衝突・・・「e≠0」だが弾性衝突とみなす
- 球①と壁の衝突・・・「e≠0」で弾性衝突でない
問題文をよく読んで注意してください。



コメント