こんにちは。Horyです。
前回の記事でガウスの法則についてまとめました。
今回の記事では導体球とガウスの法則について、電場と電位のグラフを求めます。
非常に有名な問題ですが、以下の2つで考え方が違います。
- 導体球の表面のみに電荷が分布
- 導体球の内部に電荷が分布
今回も頑張りましょう。
ガウスの法則 復習
まず、電気量Qを持つ電荷が出す電場の大きさは以下のように記述することが可能です。
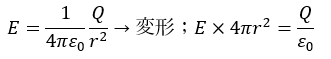
一方で、前回の記事で学んだガウスの法則は以下のように記述できます。
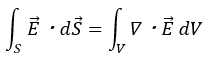
ここで、左辺の積分の中身は立体の微小面積を垂直に貫く電場の量を示していると説明しました。それを面積で積分すると言うことは・・・左辺の意味は「立体の表面積を垂直に貫く電場の量」「立体の表面積を垂直に貫く電気力線の数」と言うことができます。
この垂直に貫く量というのを電束と呼びます。
上の式は以下のように言い換えることが可能です。
「電気量Qの大きさの電荷が発生させる電場で、立体の表面積を垂直に貫く量はQ/ε0と同じ量である」
ここで、球面の半径が変わったらどうなるかを考えてみましょう。
今、半径rと半径Rの球面を考えます(r<R)。
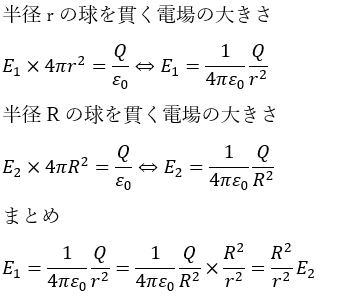
これの意味するところは、球を拡大や縮小したところで、立体の表面を垂直に貫く電気力線の数(電場の量)は変化しない⇔電束はQ/ε0で変化しないということです。
また、以下のことも重要です。
- クーロンの法則≠ガウスの法則
- クーロンの法則=ガウスの法則∩静電場が保存場
- ガウスの法則で簡単に・・・対称性が補えるとき使える (保存場である)
この保存場というのはどの方向を取っても一定の電束であるということです。
これを利用して問題に取り組みます。
問題1 電荷が分布する導体球の電場
以下に示すのは表面上に電荷が分布する導体球の電場を求める問題です。

(1)解答・解説
単位面積当たりを貫く電気力線の本数がEと約束したので・・・
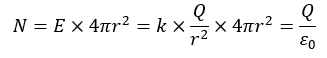
以上が解答になります。
(2)解答・解説
「表面に」一様に正電荷が分布しています。
- 導体球内部に電気力線はない
- 導体球の表面・外側に電気力線ある
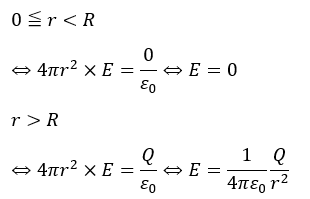
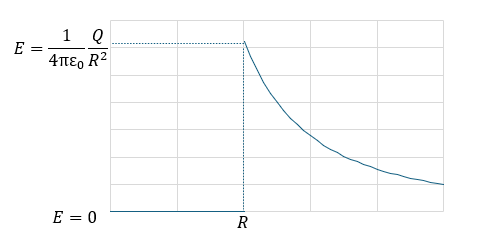
(3)解答・解説
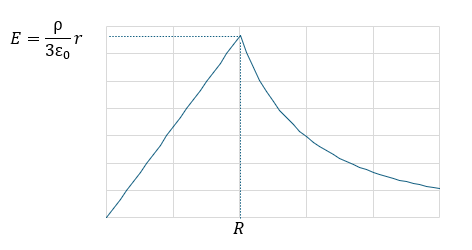
今度は表面だけでなく球全体(内部にも)に正電荷が一様に分布していて、その密度がρ[C/m3]であると書いてあります。
こういう場合、まずは、導体球全体が持つ電気量を求めましょう。
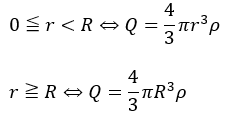
これをガウスの法則に応用すれば良いです。
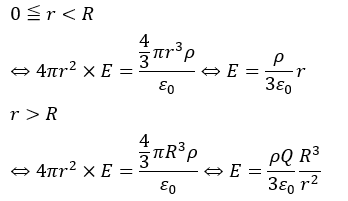
問題2 表面上に電荷が分布する導体球の電位
以下に示すのは球の表面上に電荷が分布する導体球の電位の問題です。
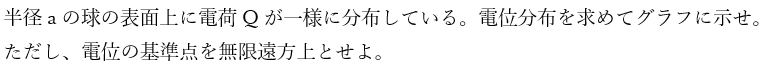
この問題を例に解説します。
- 電場の表面積分
- 総電荷/ε0
- 上の2つの量は等しい
- 電荷の位置エネルギーは
- 電荷を無限遠方より運ぶときのクーロン力による仕事に等しい

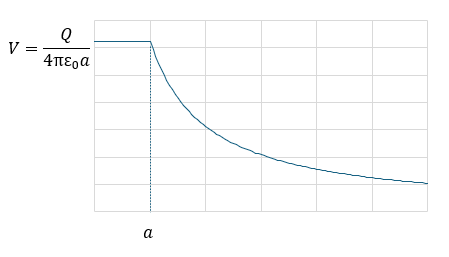
問題2 解答・解説
先ほどの電場の問題で表面上にだけ電荷が分布してるなら・・・
- 導体球の内部・・・電場は0 (電気力線ない)
- 導体球の外側・・・電場あり
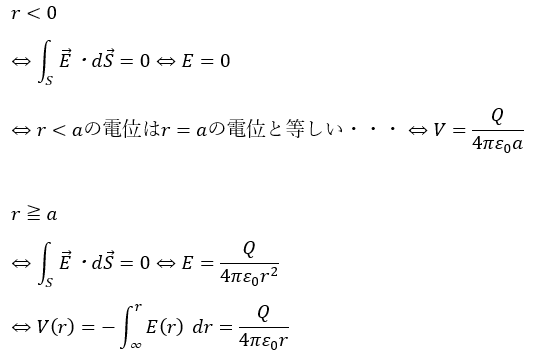
問題3 球全体に電荷が分布する導体球の電位
以下に示すのは球全体に電荷が分布する導体球の電位の問題です。
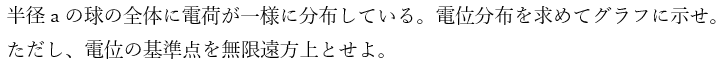
この問題を例に解説します。
問題1の(3)で電場は求めています。ただし、今回の問題では電荷密度が書かれていません。
こういう場合は、まず、電荷密度をρとしてこれを求めます。
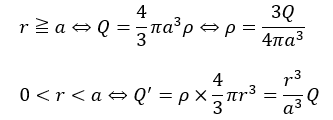
これにより、電荷密度を求めることができました。
- r≧a⇔全電気量はQである
- 0<r<a⇔電荷密度を用いて電気量を求める
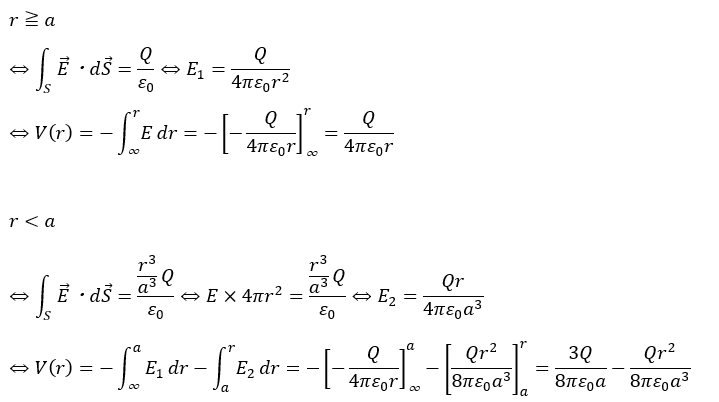
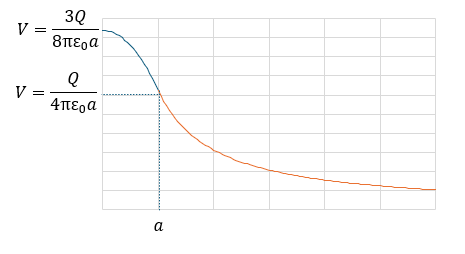
導体球の内部と外側で電場が違うということを抑えてください。
当然、r<aのときで位置エネルギーを求めるときに領域によって式が違ってきます。



コメント