こんにちは。Horyです。
前回の記事では抵抗に関する説明とオームの法則を原理から導出しました。
今回の記事では導体中の自由電子の動きに関する問題になります。前回の内容と被る部分もありますが、頑張りましょう。
導体中の自由電子の動き 問題
以下に示すのは問題です。

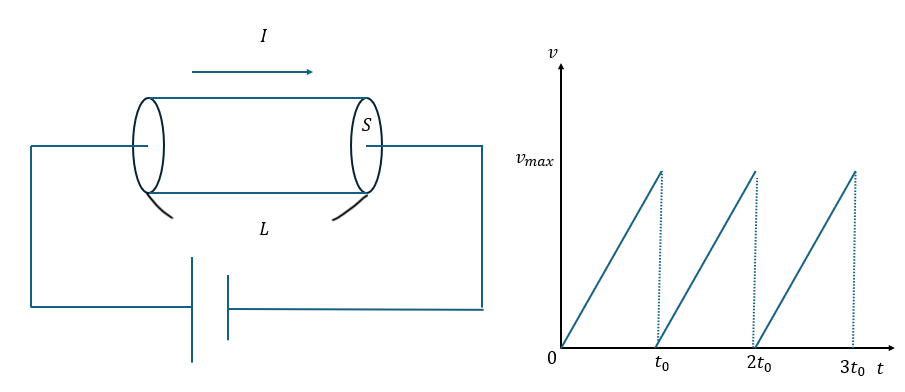
(1)・(2)解答・解説
今回は電子が速度に比例する抵抗力を受けるとは書いていないので、クーロン力だけを受けると考えればいいです。電子の加速度をaとして運動方程式を作ります。
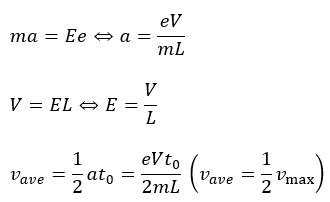
ここで、中学で習ったと思いますが、電流の正体は電荷の流れで、これは電子の流れとも言えます。
導体中の電子の運動をこの問題では「グラフのモデル」より考えます。
グラフの意味としては、「電子は時間t0加速した後、速度が0になり、再び加速して・・・」の繰り返しです。なんで、速度が急に0になるかを考えます。
これが意味するところは、自由電子が導体中の陽イオンとぶつかりながら運動しているということです。だから、速度の変化が生まれています。
ただ、実際の電子は運動が一方向だけではなく複雑です。
これをモデル化すると、電子は陽イオンとの衝突により、等方的(全ての方向に同様に確からしく)散乱しています。だから、散乱後の速度は平均して0とみなせます。
(3)解答・解説
まず、電流の向きと大きさについて、簡単に解説します。
- 電流
- 大きさ・・・単位時間当たりの通過電荷の大きさ
- 向き・・・電子の平均速度と逆の向き
微小時間Δtが経過する間に導体の注目する面を通る微小電荷Δqの大きさを考えます。
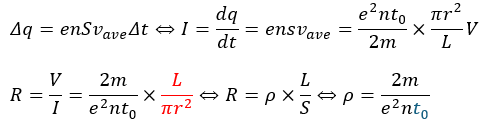
- 抵抗R・・・赤い部分より、同じ物質でも形状によって違ってくる
- 低効率ρ・・・物質が同じなら必ず同じ値になる。
ここで、「モデルを作る」とはどういうことかというと、「そのモデルを用いて測定できる物理量の論理式を用いて物理量を導出→実験と比較する」
モデルから得られた物理量と実験結果が一致することは、「その現象をモデルで説明できる」といいます。
ちなみに、抵抗率についてですが、金属の温度上昇で原子の熱振動の振幅が増えます。
これにより、電子が陽イオンに散乱される頻度が増えることで、グラフのt0が小さくなります(式の青い部分)。つまり、抵抗率が増加します。
(4)解答・解説
電場が一つの電子にする仕事率を求めて、これに電子数をかけます。
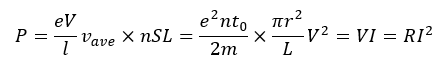
ここで、上の式の意味を言葉で説明します。
電子は電場より仕事されるが速さは一定とみなせます。
これは、同じ大きさで負の仕事を陽イオンから・正の仕事を陽イオンに与える(電場よりもらうエネルギーを消費しきっているからグラフの速度が急に0になる)
Pのことを消費電力というが、この消費によって、陽イオンの熱運動エネルギーが増えるため、Pのことを単位体積当たりのジュール熱とも言います。つまり、この消費電力は熱に変換されます。



コメント