こんにちは。Horyです。
前回の記事では接線と曲線が囲む図形の面積を求める比較的に簡単な問題を解説しました。
面積のフローチャート化の威力を学べたと思います。
今回の記事では対称性のある曲線の囲む面積を求める問題に取り組みます。
微分だけでなく積分でも曲線の対称性は非常に重要です。
今回も頑張りましょう。
対称性のある図形の面積
以下はこの記事で取り組む対称性のある曲線の面積を求める問題です。

この問題を攻略しようと思います。
問題を解く前の下準備 グラフを描く
問題を解く前の下準備です。
グラフを描けとは言われていませんが、簡単でも良いのでグラフを描いてみましょう。
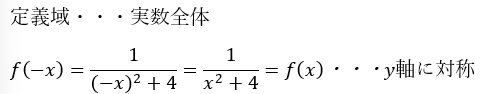
関数を微分します。Y軸について対称なのでx>0の範囲だけ考えれば良いです。
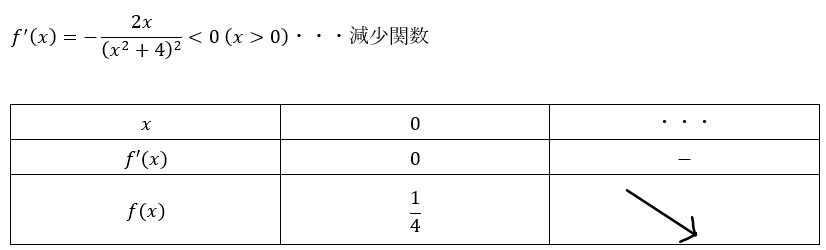
グラフを描いてみましょう。
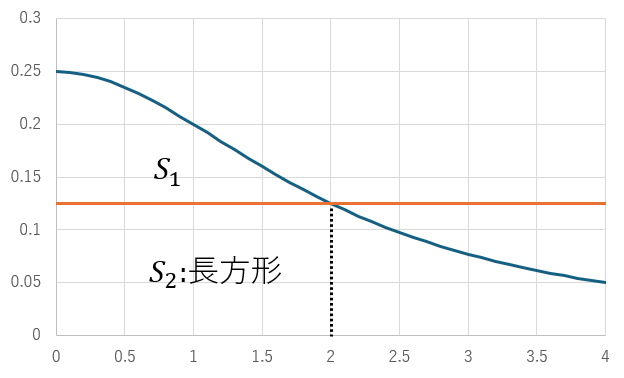
求める面積は長方形の面積S2を「曲線とx軸とy=2」が囲む面積S1から引き算すれば求めれます。
解答・解説
問題の解答・解説です。まずは、直線と曲線の交点を求めましょう。
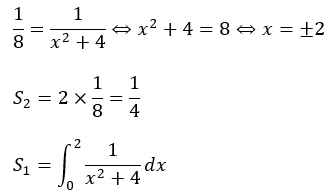
S1の積分は暗記型置き換え積分のtan型が使えます。
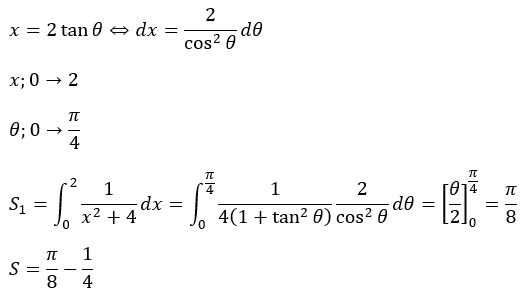
「これでできた!」と思ってここで終わってはいけません。y軸対称ということを忘れないでください。求めた面積を二倍する必要があります。
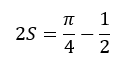
以上が解答です。



コメント