こんにちは。Horyです。
前回の記事では固体・液体の質量比熱に関する記事を記述しました。
今回の記事では定積変化と定圧変化での比熱を解説すると共にマイヤーの関係式を導出したいと思います。
今回も頑張りましょう。
比熱とは何か?
前回の記事で紹介した比熱は質量比熱と言うモノです。
念のためにおさらいします。
- 質量比熱・・・物質1gの温度を1K上昇させるために必要な熱量
- 熱容量・・・物質に投入した熱量を温度変化で割ったモノ
比熱は質量比熱のみではありません。
- モル比熱・・・物質1molの温度を1K上昇させるために必要な熱量
- →熱容量を物質量で割り算した量
質量比熱とモル比熱の違いを意識すると共に、今回紹介する定積比熱や定圧比熱はモル比熱と言うことは予め断っておきます。
比熱とは物理的に説明すると「系に流入した熱量を温度で偏微分した量」と言うことができます。
偏微分に関する記事はこちらの記事を読んでほしい限りですが・・・
変数を以下のように設定します。
- Q [J]・・・流入熱量
- P [Pa]・・・圧力
- V [m^3]・・・体積
- T [K]・・・温度
- n [mol]・・・物質量

一応、大学内容ですが、定積比熱/定圧比熱の定義になりますので覚えておいてください。
ここからマイヤーの関係式と呼ばれる定積比熱と定圧比熱の関係式を導出します。
マイヤーの関係式導出
マイヤーの関係式を導出していきます。
まずは熱力学第一法則ですが、以下のように主役と熱量の正負を定義します。
- 主役・・・系(気体)・・・「系は外力にされる」
- 正・・・外力が系にする仕事を正 「+dW」
- 式;dU = dQ – dW ⇔ dQ = dU + dW

ここで、全微分については偏微分の記事でも解説していなかったと思うので説明します。
(簡単のために二変数とします)
- 全微分(二変数)
- ある関数を二変数の関数と見る
- 一方を固定して関数を他方で偏微分した量に他方の微小変化をかける・・・①
- 他方を固定して関数を一方で偏微分した量に一方の微小変化をかける・・・②
- ①と②の両者の和・・・二変数における全微分
全微分は大学数学のみならず、大学の熱力学でも非常に重宝するので覚えておいてください。
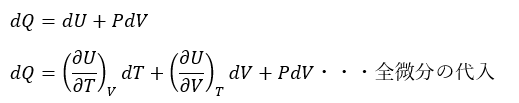
さて、ここで、定積の場合と定圧の場合とで比熱の定義を思い出してみてください。
定積変化と定積比熱

- まとめ (定積変化)
- 定積変化→系の体積が変化しない
- dV=0より仕事が0 ⇔ dU = dQ
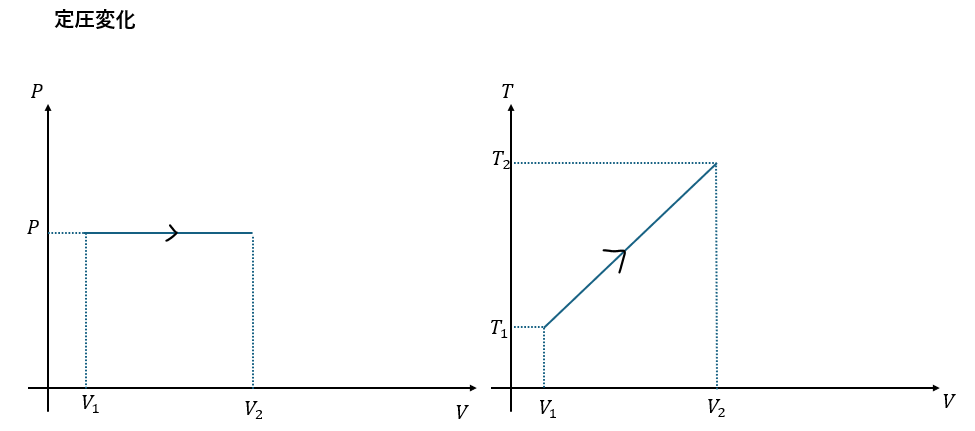
定圧変化と定圧比熱
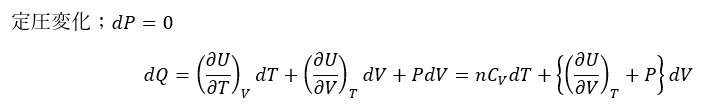
ここで、私が教えてきた大多数の大学生は手が止まります。
どうしたモノかと思いますが、Vを温度Tと圧力Pの関数と見ます(ただし、Pは定数だ)。
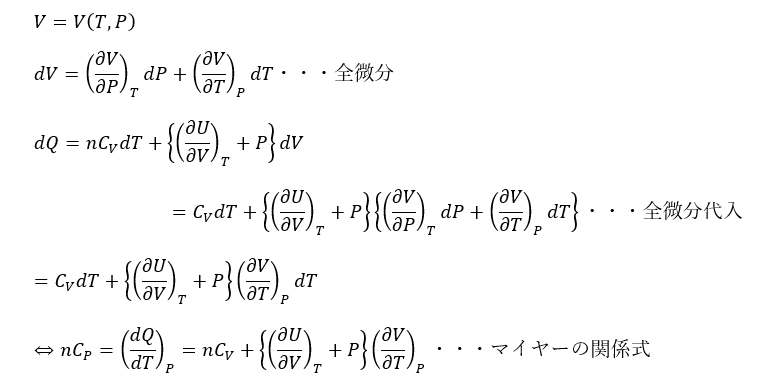
定積比熱と定圧比熱の関係式であるマイヤーの関係式を導出することに成功しました。
- まとめ
- 定圧変化→系の圧力が変化しない
- dP=0より圧力は定数と見なせる
- dW = PdV
単原子分子(理想気体)のマイヤーの関係式
単原子分子理想気体のマイヤーの関係式を考えます。
あくまで単原子分子のみに適用可能な公式です。全ての気体に適用できるわけではありません。

単原子分子理想気体の内部エネルギーは温度にのみ依存する関数です。
そのため、内部エネルギーを体積で偏微分しても0になります。
グラフでの対応
定積変化と定圧変化をグラフで対応させてみます。
覚えておくといいでしょう。
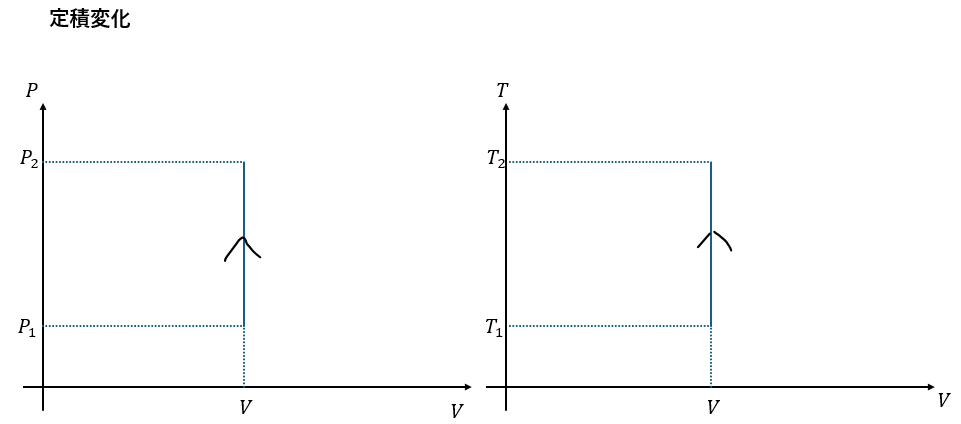


コメント