こんにちは。Horyです。
前回の記事では完全順列に関する問題の攻略を行いました。
今回の記事ではスターリング数に関する問題を攻略します。
スターリング数に関する問題は完全順列の問題と状況とかが似ることが多いので合わせて理解しておいた方が良いです。
今回も頑張りましょう。
スターリング数 問題
以下に示すのはこの記事で取り組むスターリング数に関する問題です。

この問題を例に解説します。
また、注意点ですが、場合の数は同じモノであっても区別しません。
玉に関しては番号が違うので区別出来ます。
一方で、箱に関しては番号が付いていないので区別出来ません。
ここら辺のことは以下の記事に書いてあるので読んどいてください。
上の問題の言葉を用いると、本問は「分けるモノ(玉)に区別はあるが、グループ(箱)に区別はない場合の組み分け」です。
(1)解答・解説
求める数を言葉で説明すると・・・
- 1からnの数字が書かれた玉をn-1個の箱に分割
- 1からnの数字か書かれた玉をn-2個の箱に分割
- どの箱にも玉が入る
まずは、n-1個に分割する方法ですが、これは、箱の内の1つには玉が2つ入ることになるので、「n個の玉から2つの玉を選ぶ場合の数」と同じです。
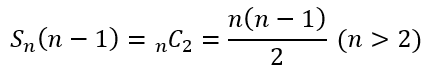
続いて、n-2個に分割する方法になります。やり方としては2つあります。
- 箱の内の1つに3個の玉が入る (他の箱には1個ずつ)・・・①
- 箱の内の2つに2個ずつ玉が入る (他の箱には1個ずつ)・・・②
- ①について、玉の数は3個以上でないと成立しません。
- ②に関しても注意です。玉の数が4個以上じゃないと成り立ちません。
まずは、①を求めていきます。
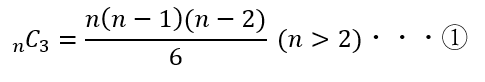
続いて、②を求めていきます。
これは、「n個の玉から2つの玉を選ぶ」⇒「n-2個の玉から2つの玉を選ぶ」場合の数を求めれば良いだけです。
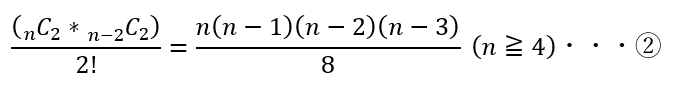
注意してほしいのが箱に番号が付いていないので2個ずつ入った2つの箱を区別することは出来ないです。
そのため、2!で割る必要性があります。
(2)解答・解説
求める場合の数は「n個の玉を2つの箱に振り分ける場合の数」になります。
ただし、0個の箱があってはなりません。
ただ、この問題は意外と曲者です。
- 玉の数が奇数;箱内の玉が同じになることはない
- 玉の数が偶数;箱内の玉が同じになることが1回だけアル
つまり、奇数の時と偶数の時で分けて考えないといけないです。

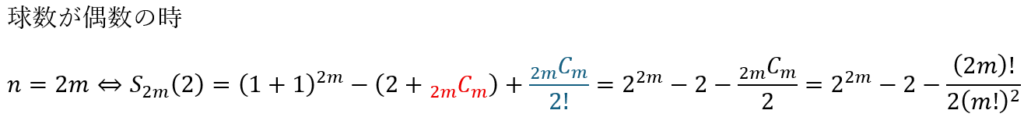
- 赤い部分;m個とm個に分けられる場合の数を一旦全部引いてる
- 青い部分;m個とm個に分けられるが、箱に区別がないので2!で割る
(3)解答・解説
登場する文字を言葉で説明してみます。
- Sn(k-1);n個の玉をk-1個の箱に分ける
- Sn(k);n個の玉をk個の箱に分ける
- Sn+1(k);n+1個の玉をk個の箱に分ける
やり方は以下に示す2つです。
- (Ⅰ);Sn(k-1)を用いる
- 特定の玉1個だけを箱に入れる
- 残りのn個の玉をk-1個の箱に分ける
- これはSn(k-1)通り
- (Ⅱ);Sn(k)を用いる
- 特定の玉1個がすでに玉が入った箱に入る
- 特定の玉以外のn個の玉をk個の箱に分ける;Sn(k)
- 上で作ったk個の箱のどれかに特定の玉を1個入れる;k通り
- これはkSn(k)通り
最終的な場合の数は以下のように表せます。
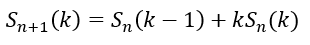
余談 (追加問題)
スターリング数には関係ない問題かもしれませんが、Sn(n-1)を求める問題について、以下の場合の数を求めてみてほしいです。
- 玉に区別があって箱に区別がない (本問)
- 玉にも箱にも区別がある
- 玉に区別はなくて箱に区別がある
- 玉にも箱にも区別がない



コメント