こんにちは。Horyです。
今回の記事では回転運動方程式とモーメントの釣り合いについて解説します。
高校物理ではモーメントの釣り合い(力のモーメント)という分野になりますが、僕は、この分野は回転運動方程式についてある程度分かっていないと理解できないのではないかと考えています。
そして、回転運動方程式は大学物理なので力のモーメントも大学内容で良いのではないかと僕は個人的に思います。
この記事を読む前に、運動方程式の極座標変換についての記事は読んでおいた方が良いと思います。
それでは、今回も頑張りましょう。
回転運動方程式
以下に示すような物体が回転運動をしていると考えます。
物体内には大量の原子が詰まっていますが、今回はその原子の中の2つをピックアップします。
また、物体の回転中心と原子間の距離をri(i=1,2,3・・・)とします。
以下に図を示します。
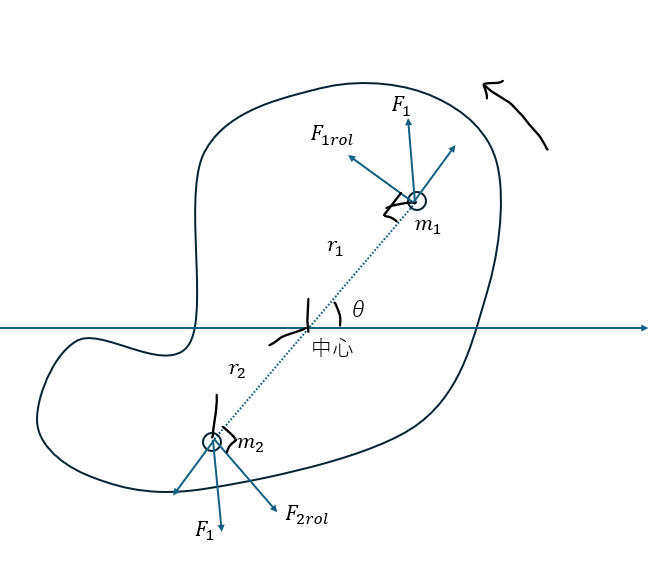
図では力をスカラー表示させていますが、物体が回転する方向(θが増える方向)を正として・・・
回転の中心について、接線方向の運動方程式を立てると・・・
原子1も原子2も回転方向の力はθを増加させる方向に向いているので・・・
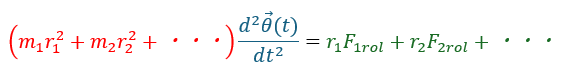
- 赤い部分・・・慣性モーメント
- 青い部分・・・角加速度
- 緑の部分・・・力のモーメント
上の式を回転運動方程式と呼んでいます。
そして、物体が回転しないとき、つまり、それぞれの原子におけるθが一定のとき、以下の式が成立します。
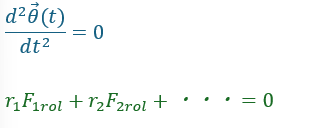
上の緑の式が0になるとき、物体は回転していないと言うことができ、このとき、「力のモーメントが釣り合っている」といいます。
大量の原子をどう処理するか・・・非接触力
先ほどの問題では2つの原子にピックアップしましたが、物体は大量の原子でできています。
原子1つ1つに運動方程式を立てていたらきりがありません(というか絶対無理)。
どうしたモノかと思いますが、試しに2つの原子で考えてみます。
以下の図のように基準点を考えて、基準点からの距離を設定します。
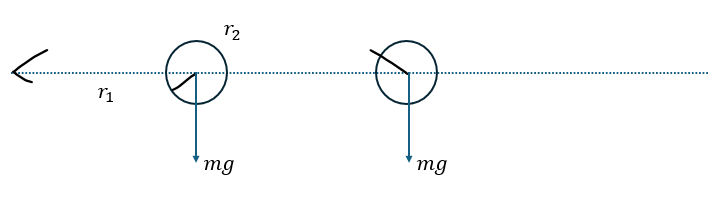
この系が原子の重力により回転を行うとします。
力のモーメントは以下のように記述することができます。ここでは、モーメントをMとします。
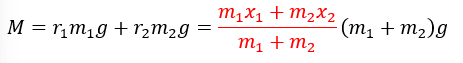
上の赤い部分で書いたところが重要で、赤い部分はこの系における重心の位置になります。
ところで、n個の原子が集まった物体を考えて、物体の質量をmとおいても・・・
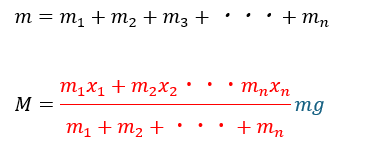
- 赤い部分・・・物体の重心
- 青い部分・・・物体が地球より受ける重力
つまり、直接的に接していない重力などの力を物体は重心で受けていると捉えてよく、これらの力のモーメントを考えるときは回転中心と重心の距離を考えれば良いということです。
(壁に立てかけられたはしごとかは壁とはしごの接点は一点に限られ、その点に壁からの抗力が及ぼされている。)
まとめ・・・
力のモーメントは今までの運動方程式とは全く異なるのでモーメントの釣り合いの式をどうやって立てれば良いか悩む学生をよく見かけます。
以下にモーメントの釣り合いの式を立てるときのポイントを示します
- 基準点の設定・・・未知力が集まる部分を基準点とした方が良い
- 基準点と力の作用点を直線で結ぶ
- 先ほどの直線に対して垂直方向と水平方向に力を分解する
- 垂直方向(接線方向)に分解した力の方向からどちら向きに回る力かを考える
- 直線について、力の水平成分の大きさと、基準点からの距離を掛ける (力のモーメント)
- モーメントが釣り合っているなら反時計回りと時計回りの力のモーメント和が等しい
以上で終わります。
まぁ、問題で慣れないことには始まらないので次回から問題です。



コメント