こんにちは。horyです。
前回の記事では正四面体の外接球・内接球・全ての辺に接する球の半径を求める問題に取り組みました。
今回の問題では四面体の外接球・内接球の半径を求める問題に取り組みます。
前回の記事でも書きましたが、空間図形の問題では以下のことが重要です。
- 断面を考えて3次元→2次元
- 自分に都合の良いように座標を設定する
座標の設定は対称性が高い立体で有効ですが、今回の問題では使おうと思えば使えるかもですが使いません。
そのため、断面を考える(対称面で切る)方法を用いて二次元にします。
四面体の問題
以下は今回の記事で取り組む問題です。

まず、以下に図形を示します。
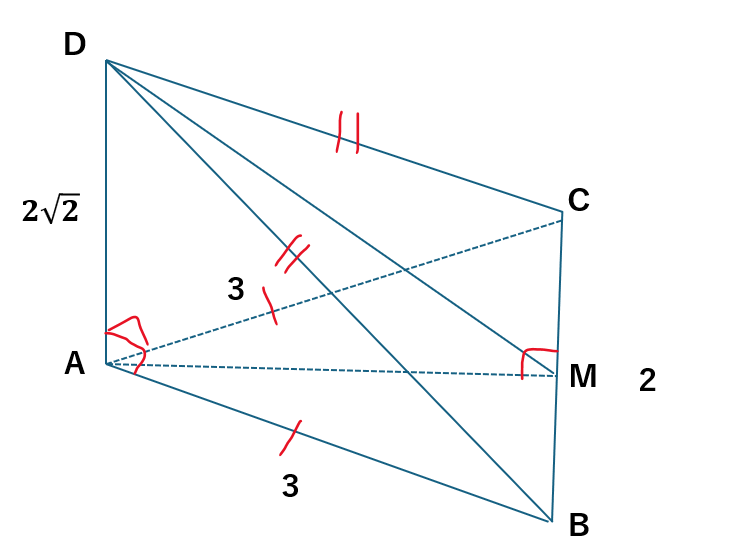
対称性のある図形を見つけることができます。
- 三角形ABC・・・二等辺三角形
- 三角形DCB・・・二等辺三角形
AからBCに引いた垂線の足とDからBCに引いた垂線の足は一致します。
これを有効的に使えるかどうかが鍵になりそうです。
外接球の半径
外接球の半径を求めます。
三角形ABCとDCBは二等辺三角形です。
ここで、三角形ABCの外接円の中心(外心)をEとします。
二等辺三角形で外心は垂直二等分線上にあるので、AM上にあります。
外接球の中心をOとします。
ここで、三角形ADMの断面を考えてみましょう。初めに断面を考えた方がOの位置関係が分かりやすいです。
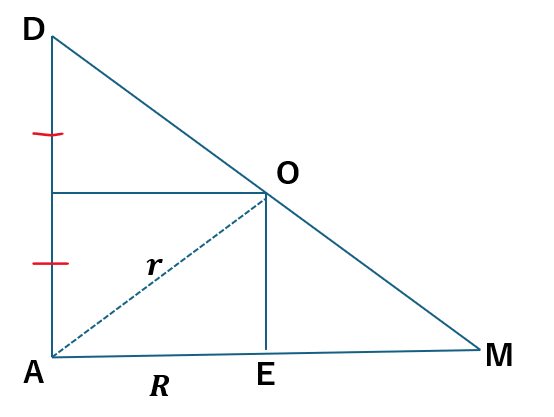
- OE⊥三角形ABC
- AD∥OE
OはADの二等分線上にあるので、Eを通り、ADに平行な直線と面DBCの交点がOです。
外接円の半径は三角形ABCの断面図・正弦定理を応用して求めれます。

外接球の半径は直角三角形OEAに三平方の定理を用いることで求めれます。
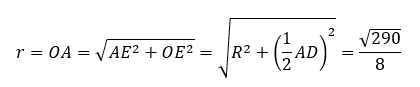
内接球の半径
内接球の半径を求めます。
どうやって求めるかについてですが、平面で内接円の半径から三角形の面積を求める方法を応用します。
以下に図を示します。
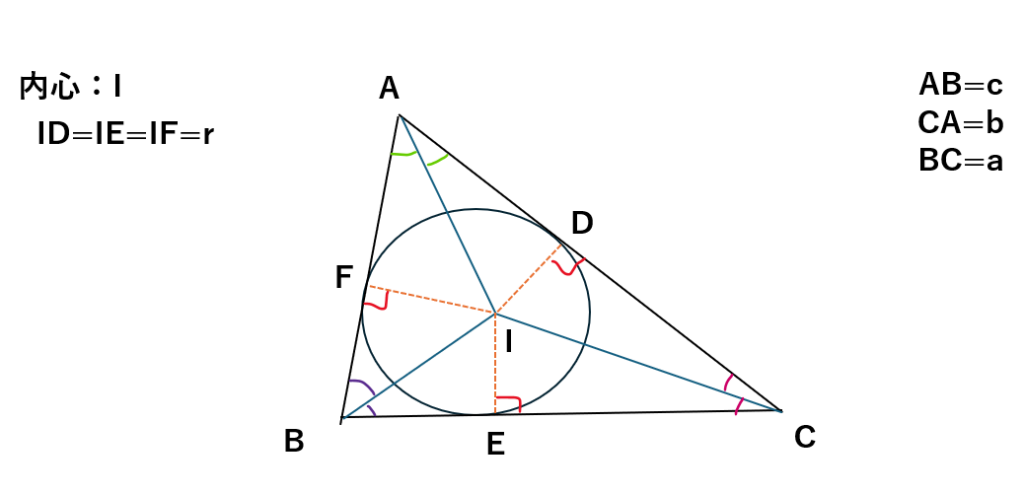
上の方法を3次元空間に応用します。
四面体ABCDの体積を二通りの方法で求めます。
- 四面体の底面と高さの公式を利用・・・①
- 四面体の表面積と内接球の半径(高さ)を利用・・・②
内接球の半径をlと考えます。
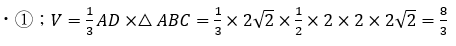
四面体の表面積をSとします。
表面積を求めるために三平方の定理を用いて辺の長さを求めます。
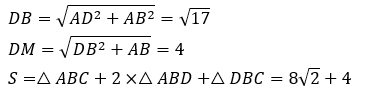
①により四面体の体積、また、上の計算により四面体の表面積が求まったので内接球の表面積を求めることができます。
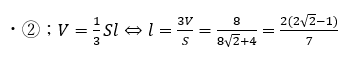



コメント