こんにちは。Horyです。
これまでに運動量保存則とエネルギー保存則に関する様々な問題に取り組んできました。
今回取り組むのは台上を動く物体についてです。
今回も頑張りましょう。
問題1 台上を動く物体
以下に示すのは台上を動く物体に関する問題1です。

この問題を例に解説します。台が動かないのでまだ厄介ではないです。
状況を以下に図示します。
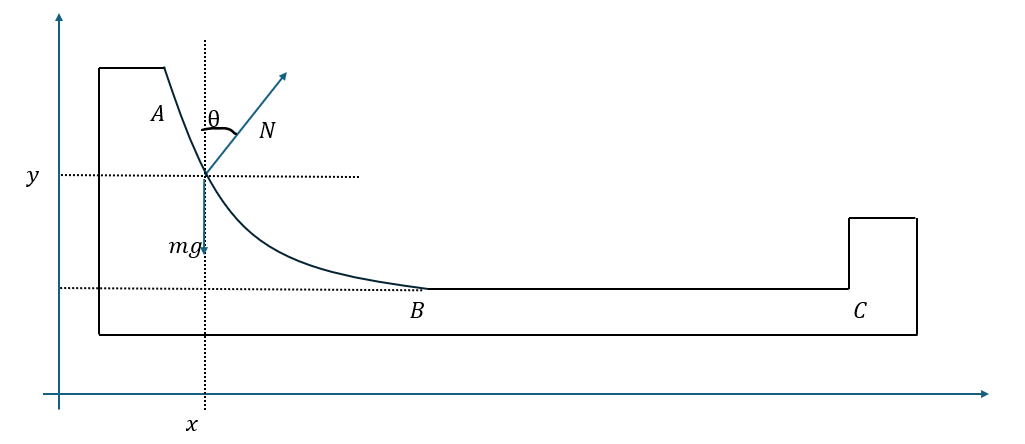
今回は台が動かないので小球についての運動方程式を成分ごとに書けば良いです。
運動方程式の記述
まずは、小球の運動方程式を示します。
物体の位置と速度をベクトルにより設定します。
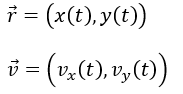
成分ごとに運動方程式を記述します。また、拘束条件についても重要です。
こちらの記事に書かれています。
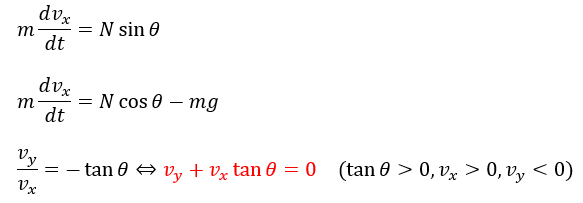
上の3つの式を利用します。これを利用すると速度についての時間追跡ができるように感じますが・・・
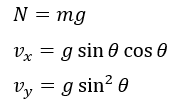
斜面が直線上の斜面ではないのでθが時間変化します。
斜面上での時間追跡はちょっと厳しそうです。
問題1 解答・解説
運動方程式による記述はできませんでしたがまるっきり無駄というわけでないです。
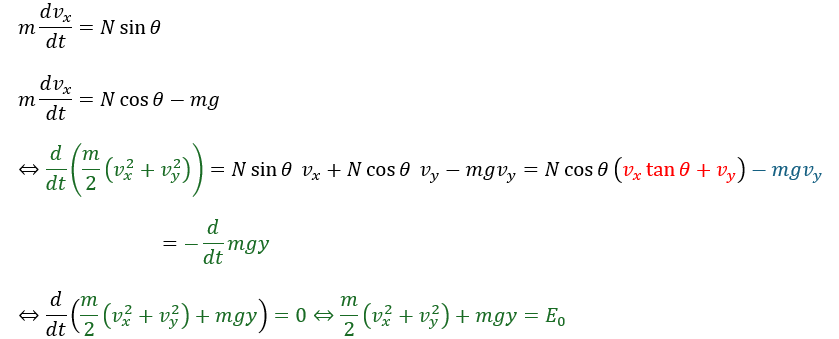
上の緑色の部分でエネルギー保存則が成立します。
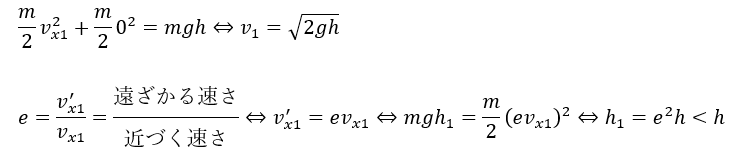
衝突後に到達する高さが落下時の高さと比較して低いです。
つまり、衝突前後で運動エネルギーが減少しています。
つまり、減った運動エネルギー分、台の内部エネルギーが増えるということです。
問題1 台上を動く物体
以下に示すのは台上を動く物体に関する問題2です。

事前準備
まずは、事前準備です。
小球についての運動方程式も書かねば行けませんが、台も動くので運動方程式を書きます。
作用反作用が鍵になってきます。以下に図を示します
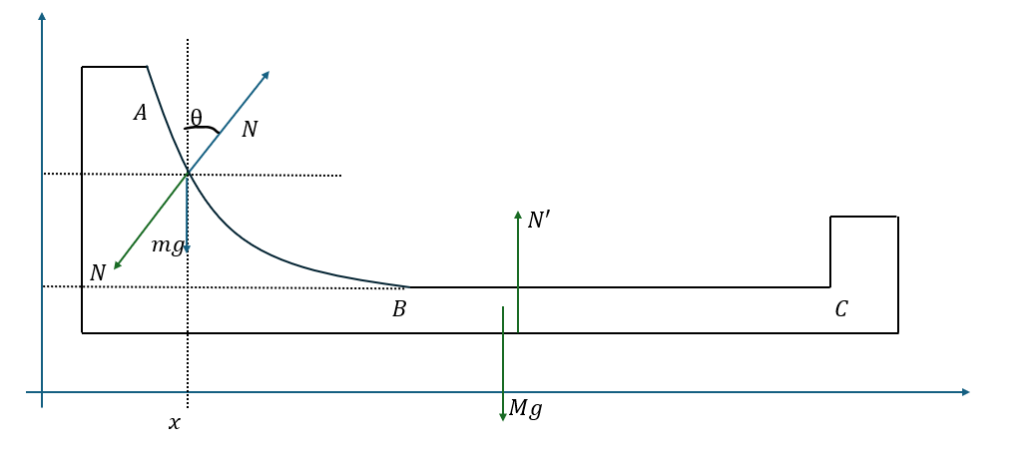
- 青の矢印・・・小球に働く力
- 緑の矢印・・・台に働く力
それでは、運動方程式を記述します。
台は水平面より離れないので台についてはy成分で力が釣り合っています。
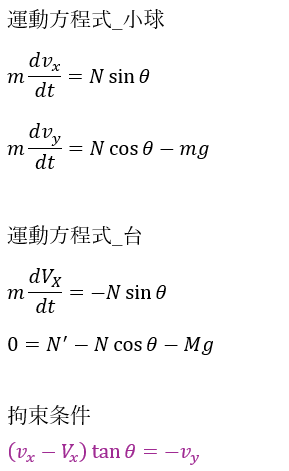
先ほどの問題と同様に、斜面が直線ではないので、斜面上での運動を記述できませんが、水平なBC上での運動は記述可能です(θ=0)。

ここから、この系の保存則を作ります。
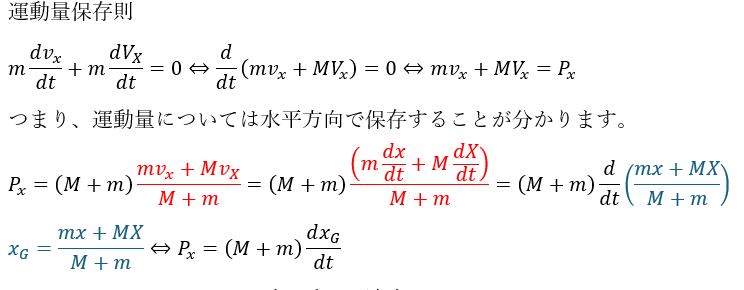
- 赤で示した部分・・・この系の重心の速度
- 青で示した部分・・・この系の重心の位置
- 外部から力が働かないならその成分について重心の速度は一定
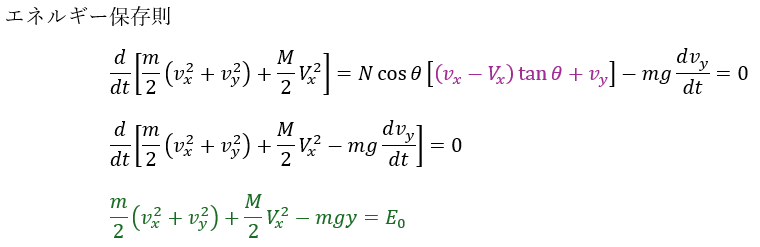
緑で書いた部分がエネルギー保存則です。ただし、衝突前後でエネルギーは変化します。これに注意してください。
これで準備は完了です。
問題2 解答・解説
- 初め・・・台;0/球;0
- 点B・・・台;V2/球v2
運動方程式とエネルギー保存則を立てます。
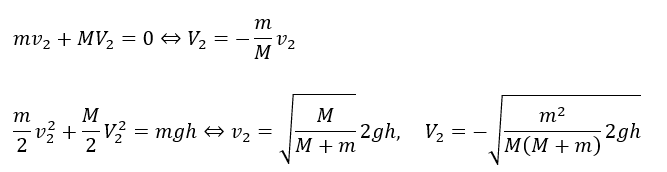
Bを通過してから壁に衝突するまでの時間を求めます。
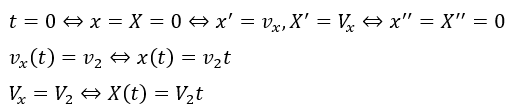
ここで、Bから壁までの距離はaだと問題文に記載されています。台と小球の進行方向(ベクトル)に気をつけてください。
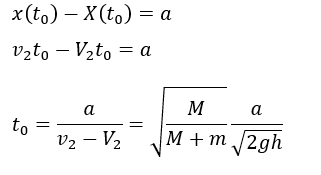
- 衝突直前・・・台;V2/球;v2
- 衝突直後・・・台;V3/球v3

続いて衝突後の最高点を考えます。
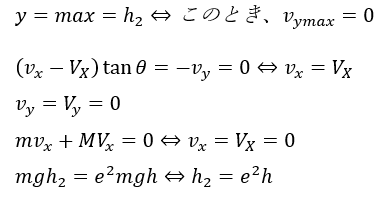



コメント