こんにちは。Horyです。
前回の記事で回転運動方程式について基本を学ぶと共に、力のモーメントが釣り合う状況について押さえたと思います。
今回の記事では力のモーメントに関して基本問題の攻略をしていこうと思います。
出題する問題のテーマは以下の通りです。
- 力のモーメントを求める
- 一様な棒を折り曲げる問題
- 穴の空いた図形の重心を求める
- 不均質な棒を持ち上げる
今回も頑張りましょう。
問題1 力のモーメントを求める
以下に示すのは力のモーメントを求める問題です。非常に簡単な問題なので問題と解答をまとめて記述します。

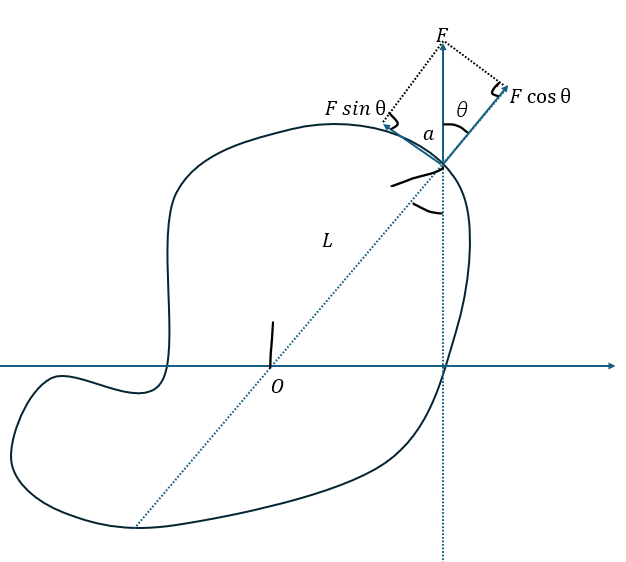
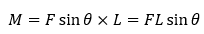
これは前回の記事をよく読めばできる問題です。
問題2 一様な棒を折り曲げる
以下に示すのは一様な棒を折り曲げる問題です。

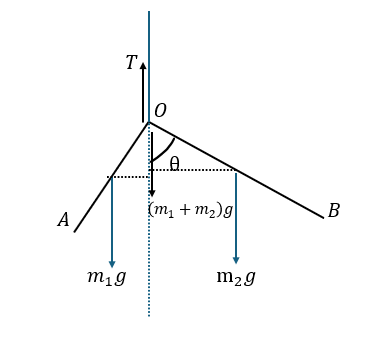
前回の記事でもやりましたが、非接触力である重力の作用点は重心です。
折り曲げられていない棒は均質で対称性があるので、重心は棒の中点になります。
問題2 解答・解説
問題2の解答・解説です。
棒を折り曲げた後のOA側とOB側に分けたいと思います。
- T・・・糸の張力
- OAの中点A1・・・OA側の重力の作用点
- OBの中点B1・・・OB側の重力の作用点
ここで、折り曲げられた棒の重心がどこにあるかわ不明です(求めれない)。
ただ、糸の張力と棒全体の重力が釣り合っているので、この作用線上のどこかに重心があることになります(図の点線部のどこか)。
ここで、重心をGとすると線分の長さについて以下に比が成立します。
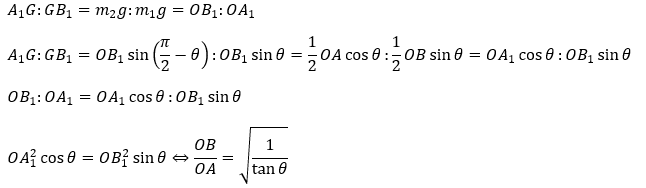
以上が解答になります。
問題3 穴の空いた図形の重心
以下に示すのは穴の空いた図形の重心を求める問題です。

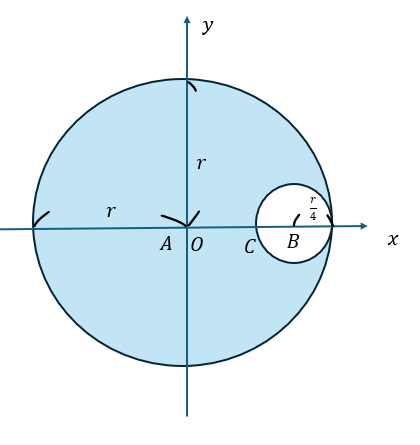
この問題を例に解説します。
問題3 解答・解説
- 切り取られた以外の部分・・・重心A/質量m1
- 切り取る円板・・・重心B/質量m2
切り取られる前の円の重心は円の中心です(当たり前)。
切り取られた後の図形はx軸について対称なので、切り取られた後の図形も重心はx軸上にあります。
- 切り取る前の図形の重心O
- 切り取られた図形の重心A
- 切り取った図形の重心B
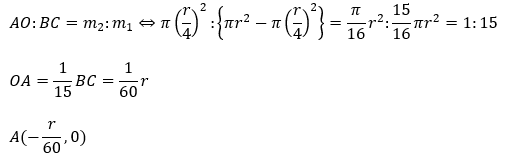
言葉で書くなら、切り取られた後の図形の重心AはOの左方、距離「r/60」の点
問題4 不均質な棒を持ち上げる
以下に示すのは不均質な棒を持ち上げる問題です。

この問題を例に解説します。以下に図を示します。
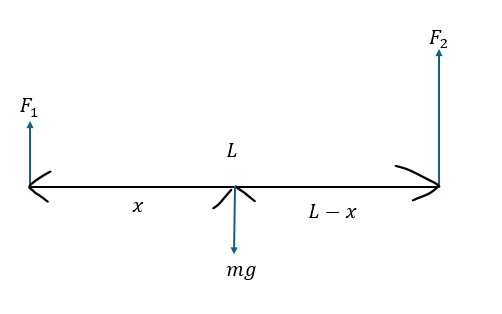
問題4 解答・解説
問題内容から棒が持ち上がる直前です。
直前と言うことは、まだ棒は水平ということにして良いです。
- x・・・棒の重心から左端までの距離
- 左端を持ち上げる・・・右端の周りでモーメントの釣り合い
- 右端を持ち上げる・・・左端の周りでモーメントの釣り合い
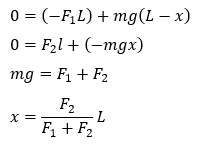



コメント