こんにちは。Horyです。
今回の記事では物理の熱力学という観点から分圧の法則とボイルの法則に関して解説しようと思います。
気体の法則等は化学の記事でも解説しましたが、、、
一部がちゃんとした証明にはなってない(感覚的な証明になっている)と思いますのでこの記事ではそこら辺から掘り下げようと思います。
今回も頑張りましょう。
分圧の法則
分圧の法則について解説します。
分圧の法則とは、容器内に混合気体が入っているとして、全圧がPだとしたら、「混合気体の分圧を全て足し上げると全圧になる」というのが分圧の法則です。
これを式で証明してみたいと思います。
ところで、気体分子運動論の記事で次のような式が登場したことを覚えていますでしょうか?

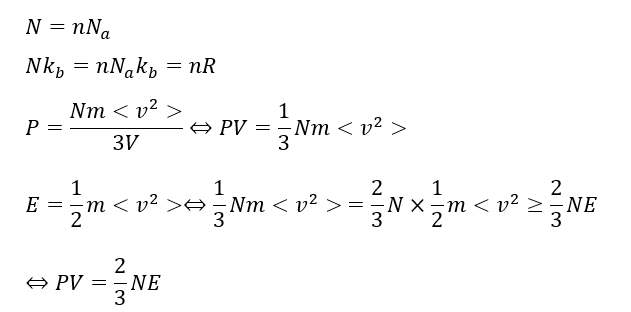
- N・・・気体の全粒子数
- Na・・・アボガドロ数
- n・・・物質量
- <v>・・・粒子の速度の平均値
- E・・・粒子の運動エネルギー
ここまでは気体分子運動論でやった内容でこれを利用していきます。
混合気体と個別気体について以下のように定義します。
- 混合気体について・・・
- N・・・全粒子数
- P・・・全圧
- <E>・・・一分子の平均運動エネルギー
- V・・・体積
- 個別の気体について・・・
- Ni・・・分子数
- Pi・・・圧力(分圧)
- <εi>・・・一分子の平均運動エネルギー

ここで、今後気体の平均運動エネルギーは以下のように表すことができます(当然の割り算)。
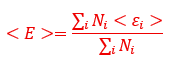
さて、「個別気体に関する式」と「混合気体に関する式」を変形してみます。
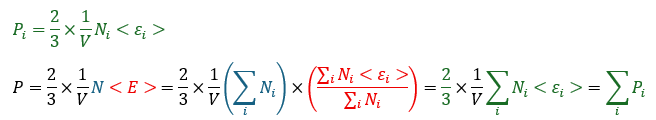
以上より、確かに混合気体の分圧を全て足すと全圧になることが物理的に明らかになりました(体積は一定)。
ボイルの法則の導出
分圧の法則の導出に成功したのでボイルの法則も芋づる式に導出できます。
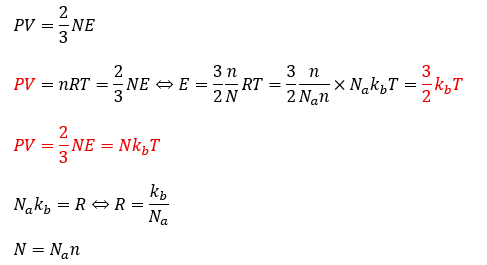
上の式の赤い部分に注目してほしいです。エネルギーが温度にのみ依存する関数になっております。
そのため、温度が一定であればPVは一定と言うことが明らかとなり、ボイルの法則が証明されました。
理想気体の状態方程式
ボイルの法則以外にもシャルルの法則やアボガドロの法則、状態方程式等の色々な法則がありますが、これらはすでに化学の記事で解説していますので化学の記事を読んでいただきたいです。
そのため、理想気体の状態方程式に関しては上の記事を読んだという前提で話を進めていきます(この記事では解説しません)。
予めご了承ください。


コメント